题目内容
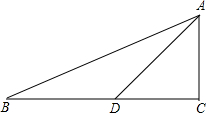 如图,在Rt△ABC中,∠C=90°,sinB=
如图,在Rt△ABC中,∠C=90°,sinB=| 5 |
| 13 |
考点:解直角三角形
专题:
分析:过D点作DE⊥AB,交AB于E点.把∠BAD构造到了直角三角形中,要求∠BAD的正切值,只需求得DE,AE的长.根据等腰直角三角形的性质可以求得AC,AD的长,在直角三角形ABC中,根据sinB=
,可以求得AB的长,根据勾股定理进一步求得BC的长,从而求得BD的长,在直角△BDE中,根据sinB=
,D可以进一步求得DE的长,根据勾股定理求得BE的长,即可进行计算.
| 5 |
| 13 |
| 5 |
| 13 |
解答: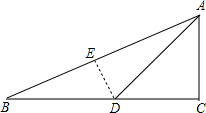 解:过D点作DE⊥AB,交AB于E点,
解:过D点作DE⊥AB,交AB于E点,
在Rt△ADC中,∠C=90°,∠ADC=45°,AC=5,
∴∠DAC=45°,
∴AC=DC=5,∴AD=5
在Rt△ABC中,∠C=90°,
∵sinB=
,
∴
=
,即
=
,
解得,AB=13.
根据勾股定理,得BC=12,
∴BD=BC-DC=12-5=7.
在Rt△BDE中,∠BED=90°,sinB=
,
∴
=
,DE=
,
在直角△AED中,根据勾股定理,得
AE=
=
∴tan∠BAD=
=
=
.
 解:过D点作DE⊥AB,交AB于E点,
解:过D点作DE⊥AB,交AB于E点,在Rt△ADC中,∠C=90°,∠ADC=45°,AC=5,
∴∠DAC=45°,
∴AC=DC=5,∴AD=5
| 2 |
在Rt△ABC中,∠C=90°,
∵sinB=
| 5 |
| 13 |
∴
| AC |
| AB |
| 5 |
| 13 |
| 5 |
| AB |
| 5 |
| 13 |
解得,AB=13.
根据勾股定理,得BC=12,
∴BD=BC-DC=12-5=7.
在Rt△BDE中,∠BED=90°,sinB=
| 5 |
| 13 |
∴
| DE |
| BD |
| 5 |
| 13 |
| 35 |
| 13 |
在直角△AED中,根据勾股定理,得
AE=
| AD2-ED2 |
| 85 |
| 13 |
∴tan∠BAD=
| ED |
| AE |
| ||
|
| 7 |
| 17 |
点评:本题考查了解直角三角形.能够巧妙作垂线,构造直角三角形.根据等腰直角三角形的性质和锐角三角函数的概念和勾股定理可以由已知的线段求得该图中所有的未知线段.

练习册系列答案
相关题目
 画如图的三视图.
画如图的三视图.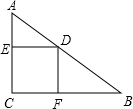 如图,在Rt△ABC中,AC=3cm,BC=4cm,四边形CFDE为矩形,其中CF,CE在两直角边上.设矩形的一边CF=xcm.当x取何值时,矩形ECFD的面积S最大?最大是多少?
如图,在Rt△ABC中,AC=3cm,BC=4cm,四边形CFDE为矩形,其中CF,CE在两直角边上.设矩形的一边CF=xcm.当x取何值时,矩形ECFD的面积S最大?最大是多少? 已知:如图,点M是弧BC的中点,点A在⊙O上,AM交BC于点D.
已知:如图,点M是弧BC的中点,点A在⊙O上,AM交BC于点D.