题目内容
19.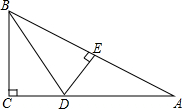 如图,在△ABC中,∠C=90°,BD平分∠ABC,DE⊥AB于E,若△BCD与△BCA的面积比为3:8,则△ADE与△BCA的面积之比1:4.
如图,在△ABC中,∠C=90°,BD平分∠ABC,DE⊥AB于E,若△BCD与△BCA的面积比为3:8,则△ADE与△BCA的面积之比1:4.
分析 求出∠CBD=∠EBD,∠C=∠BED=90°,证△BCD≌△BED,推出△CBD和△EBD的面积相等,求出四边形BCDE与△ABC的面积之比为6:8=3:4,即可得出答案.
解答 解:∵在△ABC中,∠C=90°,BD平分∠ABC交AC于点D,DE⊥AB,
∴∠CBD=∠EBD,∠C=∠BED=90°,
在△BCD和△BED中,
$\left\{\begin{array}{l}{∠C=∠BED}\\{∠CBD=∠EBD}\\{BD=BD}\end{array}\right.$,
∴△BCD≌△BED(AAS),
∴△CBD和△EBD的面积相等,
∵△BCD与△ABC的面积之比为3:8,
∴四边形BCDE与△ABC的面积之比为6:8=3:4,
∴△ADE与△ABC的面积之比为1:4.
故答案为1:4.
点评 本题考查了角平分线的性质,全等三角形的面积的应用,解此题的关键是求出四边形BCDE与△ABC的面积之比为6:8.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.自进入秋季以来起,因为天气原因,更多人选择了戴口罩,为了满足市场需求,某厂家生产A、B两种款式的环保口罩,每天共生产500个,两种口罩的成本和售价如下表
若设每天生产A口罩x个.
(1)用含x的代数式表示该工厂每天的生产成本,并进行化简;
(2)用含x的代数式表示该工厂每天获得的利润,并将所列代数式进行化简;(利润=售价-成本)
(3)当x=300时,求每天的生产成本与获得的利润.
| 成本(元/个) | 售价(元/个) | |
| A | 5 | 8 |
| B | 7 | 9 |
(1)用含x的代数式表示该工厂每天的生产成本,并进行化简;
(2)用含x的代数式表示该工厂每天获得的利润,并将所列代数式进行化简;(利润=售价-成本)
(3)当x=300时,求每天的生产成本与获得的利润.
4.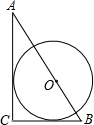 如图,Rt△ABC中,∠C=90°,O是AB边上一点,⊙O与AC、BC都相切.若BC=6,AC=8,则⊙O的半径为( )
如图,Rt△ABC中,∠C=90°,O是AB边上一点,⊙O与AC、BC都相切.若BC=6,AC=8,则⊙O的半径为( )
 如图,Rt△ABC中,∠C=90°,O是AB边上一点,⊙O与AC、BC都相切.若BC=6,AC=8,则⊙O的半径为( )
如图,Rt△ABC中,∠C=90°,O是AB边上一点,⊙O与AC、BC都相切.若BC=6,AC=8,则⊙O的半径为( )| A. | $\frac{24}{7}$ | B. | 4 | C. | 5 | D. | 2 |
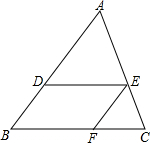 如图,在三角形ABC中,DE∥BC,EF∥AB,AD:DB=3:2,BC=25,求FC的长.
如图,在三角形ABC中,DE∥BC,EF∥AB,AD:DB=3:2,BC=25,求FC的长.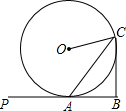 如图,AB为⊙O的切线,A为切点,点C在⊙O上,BC⊥PB于点 B,OC为⊙O的半径.
如图,AB为⊙O的切线,A为切点,点C在⊙O上,BC⊥PB于点 B,OC为⊙O的半径.