题目内容
9.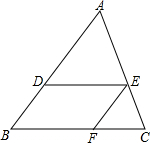 如图,在三角形ABC中,DE∥BC,EF∥AB,AD:DB=3:2,BC=25,求FC的长.
如图,在三角形ABC中,DE∥BC,EF∥AB,AD:DB=3:2,BC=25,求FC的长.
分析 由DE∥BC,EF∥AB,根据平行线分线段成比例定理,易证得$\frac{FC}{BF}=\frac{BD}{AD}$=$\frac{2}{3}$,即可求得FC:BC=2:5,又由BC=25,即可求得FC的长.
解答 解:∵AD:DB=3:2,
∴BD:AD=2:3,
∵DE∥BC,EF∥AB,
∴$\frac{EC}{AE}=\frac{BD}{AD}$,$\frac{EC}{AE}=\frac{FC}{BF}$,
∴$\frac{FC}{BF}=\frac{BD}{AD}$=$\frac{2}{3}$,
∴FC:BC=2:5,
即$\frac{FC}{25}=\frac{2}{5}$,
∴FC=10.
点评 此题考查了平行线分线段成比例定理.此题难度不大,解题的关键是注意比例变形与数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
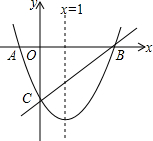 如图,对称轴为直线x=1的抛物线y=ax2+bx+c交x轴于A,B,交y轴的负半轴于C,A的坐标为(-1,0),OA=$\frac{1}{3}$OC.
如图,对称轴为直线x=1的抛物线y=ax2+bx+c交x轴于A,B,交y轴的负半轴于C,A的坐标为(-1,0),OA=$\frac{1}{3}$OC.



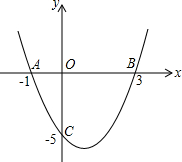 如图:已知二次函数的图象经过点A(-1,0),B(3,0),C(0,-5),
如图:已知二次函数的图象经过点A(-1,0),B(3,0),C(0,-5),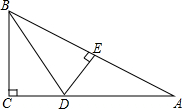 如图,在△ABC中,∠C=90°,BD平分∠ABC,DE⊥AB于E,若△BCD与△BCA的面积比为3:8,则△ADE与△BCA的面积之比1:4.
如图,在△ABC中,∠C=90°,BD平分∠ABC,DE⊥AB于E,若△BCD与△BCA的面积比为3:8,则△ADE与△BCA的面积之比1:4.