题目内容
2.不等式组$\left\{\begin{array}{l}{x+3>0}\\{1-\frac{1}{2}x≥0}\end{array}\right.$的解集在数轴上可表示为( )| A. | 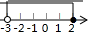 | B. |  | C. |  | D. | 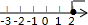 |
分析 先求出不等式组中每一个不等式的解集,再求出它们的公共部分,然后把不等式的解集表示在数轴上即可.
解答 解:由x+3>0,解得x>-3;
由1-$\frac{1}{2}$x≥0,解得x≤2,
不等式组的解集为-3<x≤2,
故选:A.
点评 本题考查了在数轴上表示不等式的解集,每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.

练习册系列答案
相关题目
11.下列说法正确的是( )
| A. | 近似数2.12万精确到十分位 | |
| B. | 经过两点有且只有一条直线 | |
| C. | 若ax=bx,则a=b | |
| D. | 若多项式5x|m|y2-(m-2)xy是四次二项式,则m=±2 |




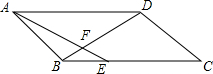 如图,E是平行四边形ABCD的边BC上一点,且$\frac{BE}{EC}$=$\frac{1}{2}$,对角线BD与AE相交于F,已知S△BEF=2,则S△ABD=24.
如图,E是平行四边形ABCD的边BC上一点,且$\frac{BE}{EC}$=$\frac{1}{2}$,对角线BD与AE相交于F,已知S△BEF=2,则S△ABD=24. 菱形ABCD的对角线AC、BD的长分别为4和2,若直线l满足:①点A到直线l的距离为$\sqrt{3}$;②B、D两点到直线l的距离相等.则符合题意的直线l的条数为( )
菱形ABCD的对角线AC、BD的长分别为4和2,若直线l满足:①点A到直线l的距离为$\sqrt{3}$;②B、D两点到直线l的距离相等.则符合题意的直线l的条数为( ) 如图,点P在∠AOB的平分线上,若使△AOP≌△BOP,则需添加的一个条件是 .
如图,点P在∠AOB的平分线上,若使△AOP≌△BOP,则需添加的一个条件是 .