题目内容
12.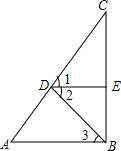 如图,∠1=∠2,DE⊥BC,AB⊥BC,求证:∠A=∠3.
如图,∠1=∠2,DE⊥BC,AB⊥BC,求证:∠A=∠3.证明:∵DE⊥BC,AB⊥BC(已知)
∴∠DEC=∠ABC=90°(垂直的定义)
∴DE∥AB(同位角相等,两直线平行)
∴∠2=∠3(两直线平行,内错角相等)
∴∠1=∠A(两直线平行,同位角相等)
又∵∠1=∠2(已知)
∴∠A=∠3.
分析 先根据垂直定义得到∠DEC=∠ABC=90°,则利用平行线的判定可得DE∥AB,然后根据平行线得性质得到∠2=∠3,∠1=∠A,再利用等量代换可得∠A=∠3.
解答 证明:∵DE⊥BC,AB⊥BC(已知)
∴∠DEC=∠ABC=90°(垂直的定义),
∴DE∥AB(同位角相等,两直线平行),
∴∠2=∠3(两直线平行,内错角相等),
∴∠1=∠A(两直线平行,同位角相等),
又∵∠1=∠2(已知),
∴∠A=∠3.
故答案为:垂直的定义;同位角相等,两直线平行;3,两直线平行,内错角相等;A,两直线平行,同位角相等.
点评 本题考查了平行线的判定与性质:平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.应用平行线的判定和性质定理时,一定要弄清题设和结论,切莫混淆.

练习册系列答案
相关题目
20. 一架2.5米长的梯子底部距离墙脚0.7米,若梯子的顶端下滑0.4米,那么梯子的底部在水平方向滑动了( )
一架2.5米长的梯子底部距离墙脚0.7米,若梯子的顶端下滑0.4米,那么梯子的底部在水平方向滑动了( )
 一架2.5米长的梯子底部距离墙脚0.7米,若梯子的顶端下滑0.4米,那么梯子的底部在水平方向滑动了( )
一架2.5米长的梯子底部距离墙脚0.7米,若梯子的顶端下滑0.4米,那么梯子的底部在水平方向滑动了( )| A. | 1.5米 | B. | 0.9米 | C. | 0.8米 | D. | 0.5米 |
4.据海关统计,2015年前两个月,我国进出口总值为37900亿元人民币,将37900用科学记数法表示为( )
| A. | 3.79×102 | B. | 0.379×105 | C. | 3.79×104 | D. | 379×102 |
1.2015年清明小长假延庆县的旅游收入约为1900万,将1900用科学记数法表示应为( )
| A. | 19×102 | B. | 1.9×103 | C. | 1.9×104 | D. | 0.19×104 |
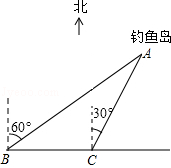 如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行50海里与钓鱼岛A的距离最近?
如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行50海里与钓鱼岛A的距离最近?
 抛物线C1:y=$\frac{1}{2}{x^2}$+bx+c与y轴交于点C(0,3),其对称轴与x轴交于点A(2,0).
抛物线C1:y=$\frac{1}{2}{x^2}$+bx+c与y轴交于点C(0,3),其对称轴与x轴交于点A(2,0).