题目内容
已知二次函数y=-x2.
(1)当0<x<2时,求y的取值范围;
(2)当-3<x<2时,求y的取值范围.
(1)当0<x<2时,求y的取值范围;
(2)当-3<x<2时,求y的取值范围.
考点:二次函数的性质
专题:
分析:(1)由二次函数y=-x2的对称轴为y轴,根据二次函数的性质:当a<0时,在对称轴的右侧,y随x的增大而减小,即可求出当0<x<2时,y的取值范围;
(2)先由二次函数y=-x2的对称轴为y轴,再根据二次函数的增减性求出最小值和最大值即可.
(2)先由二次函数y=-x2的对称轴为y轴,再根据二次函数的增减性求出最小值和最大值即可.
解答:解:∵y=-x2,
∴抛物线对称轴为y轴,即直线x=0,开口向下.
(1)∵0<x<2,
∴x=0时,函数y有最大值0;x=2时,y=-4,
∴当0<x<2时,-4<y<0;
(2)∵-3<x<2,
∴x=0时,函数y有最大值0;x=3时,y=-9,
∴当-3<x<2时,-9<y≤0.
∴抛物线对称轴为y轴,即直线x=0,开口向下.
(1)∵0<x<2,
∴x=0时,函数y有最大值0;x=2时,y=-4,
∴当0<x<2时,-4<y<0;
(2)∵-3<x<2,
∴x=0时,函数y有最大值0;x=3时,y=-9,
∴当-3<x<2时,-9<y≤0.
点评:本题考查了二次函数的性质,主要利用了二次函数的增减性和对称性,确定出对称轴从而判断出取得最大值和最小值的情况是解题的关键.

练习册系列答案
相关题目
下列选项中的算式,其计算结果是负数的是( )
| A、(-1)×(+2)×0 |
| B、(-0.5)÷(-1.84) |
| C、(-5)+(-6) |
| D、-1+1 |
 如图,梯形ABCD的上底AD长24cm,EF长36cm,如果EF与上、下底平行,那么下底BC的长度为多少?
如图,梯形ABCD的上底AD长24cm,EF长36cm,如果EF与上、下底平行,那么下底BC的长度为多少?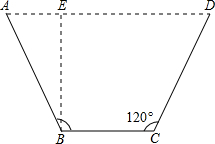 用一块宽度为5m的矩形铁皮弯折成如图所示的等腰梯形流水槽,要使流水槽的横截面面积最大,弯折的长度(梯形的腰)应为多少?
用一块宽度为5m的矩形铁皮弯折成如图所示的等腰梯形流水槽,要使流水槽的横截面面积最大,弯折的长度(梯形的腰)应为多少? 如图,若点C是AB的黄金分割点.AB=2,则AC=
如图,若点C是AB的黄金分割点.AB=2,则AC=