Question

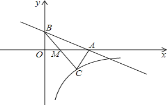
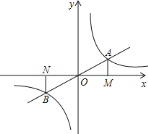
【题目】如图，正比例函数的图象与反比例函数在第一象限的图象交于点，过点作轴的垂线，垂足为，已知的面积为．

求反比例函数的解析式；

如图，点为反比例函数在第三象限图象上的点，过点作轴的垂线，垂足为，求证：．

Answer 1

【答案】；证明见解析.

【解析】

（1）根据反比例函数的比例系数的几何意义可以求得反比例函数的解析式；

（2）两函数的解析式联立组成方程组即可求得点A的坐标，进而得到ON=OM=2，NB=AM=1，∠B N O=∠AMO=90°，然后可以得到△OAM≌△OBN．

（1）设A点的坐标为（a，b），则．∴ab=k．

∵，∴，∴k=2，∴反比例函数的解析式为．

（2）由得：

∴A为（2，1）．

由反比例函数的中心对称性可得B（﹣2，﹣1），得到ON=OM=2，NB=AM=1，∠BNO=∠AMO=90°，∴△OAM≌△OBN．