Question

2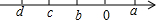．有理数a，b，c，d在数轴上的位置如图所示．试确定下面两小题的符号：
（1）$\frac{a+d}{b}$；
（2）$\frac{b-c}{d-b}$×ab．

Answer 1

分析 （1）根据图形判断出a＞0，d＜c＜b＜0，|a|=|b|＜|c|＜|d|，则a+d＜0，得出$\frac{a+d}{a}$＜0
（2）根据图形判断出a＞0，d＜c＜b＜0，|a|=|b|＜|c|＜|d|，则b-c＞0，d-b＜0，ab＜0，得出$\frac{b-c}{d-b}$×ab＞0．

解答 解：（1）由图形可得：a＞0，d＜c＜b＜0，|a|=|b|＜|c|＜|d|
则a+d＜0，
所以，$\frac{a+d}{a}$＜0
（2）由图形可得：a＞0，d＜c＜b＜0，|a|=|b|＜|c|＜|d|
则b-c＞0，d-b＜0，ab＜0，
所以，$\frac{b-c}{d-b}$×ab＞0．

点评 此题考查了数轴，解题的关键是根据图形判断出a，b的符号以及a+b、b-c、d-b以及ab与零之间的关系，再进行计算．