题目内容
8.如图,纸片ABCD是一张平行四边形纸片,要求利用所学知识作出一个菱形,甲、乙两位同学的作法分别如下:
对于甲、乙两人的作法,判断正确的为( )
| A. | 甲正确,乙错误 | B. | 甲错误,乙正确 | C. | 甲、乙均正确 | D. | 甲、乙均错误 |
分析 首先证明△AOE≌△COF(ASA),可得AE=CF,再根据一组对边平行且相等的四边形是平行四边形可判定判定四边形AECF是平行四边形,再由AC⊥EF,可根据对角线互相垂直的四边形是菱形判定出AECF是菱形;四边形ABCD是平行四边形,可根据角平分线的定义和平行线的定义,求得AB=AF,所以四边形ABEF是菱形.
解答 解:甲的作法正确;
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠ACB,
∵EF是AC的垂直平分线,
∴AO=CO,
在△AOE和△COF中,
∵$\left\{\begin{array}{l}{∠EAO=∠BCA}\\{AO=CO}\\{∠AOE=∠COF}\end{array}\right.$,
∴△AOE≌△COF(ASA),
∴AE=CF,
又∵AE∥CF,
∴四边形AECF是平行四边形,
∵EF⊥AC,
∴四边形AECF是菱形;
乙的作法正确;
∵AD∥BC,
∴∠1=∠2,∠6=∠7,
∵BF平分∠ABC,AE平分∠BAD,
∴∠2=∠3,∠5=∠6,
∴∠1=∠3,∠5=∠7,
∴AB=AF,AB=BE,
∴AF=BE
∵AF∥BE,且AF=BE,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴平行四边形ABEF是菱形.
故选C.
点评 此题主要考查了菱形形的判定,关键是掌握菱形的判定方法,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
13.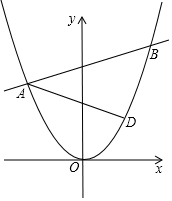 如图,点D(2,2)在抛物线y=$\frac{1}{2}$x2上,直线AB:y=kx+b交抛物线于A、B两点(A、B不与点D重合).若∠ADB=90°.求证:直线AB过定点,并求出该定点的坐标.
如图,点D(2,2)在抛物线y=$\frac{1}{2}$x2上,直线AB:y=kx+b交抛物线于A、B两点(A、B不与点D重合).若∠ADB=90°.求证:直线AB过定点,并求出该定点的坐标.
 如图,点D(2,2)在抛物线y=$\frac{1}{2}$x2上,直线AB:y=kx+b交抛物线于A、B两点(A、B不与点D重合).若∠ADB=90°.求证:直线AB过定点,并求出该定点的坐标.
如图,点D(2,2)在抛物线y=$\frac{1}{2}$x2上,直线AB:y=kx+b交抛物线于A、B两点(A、B不与点D重合).若∠ADB=90°.求证:直线AB过定点,并求出该定点的坐标.
17.函数y=kx-k的图象可能是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,在四边形ABCD中,AD∥BC,AM⊥BC,垂足为M,AN⊥DC,垂足为N,若∠BAD=∠BCD,AM=AN,AC=6,BD=8,求AM.
如图,在四边形ABCD中,AD∥BC,AM⊥BC,垂足为M,AN⊥DC,垂足为N,若∠BAD=∠BCD,AM=AN,AC=6,BD=8,求AM.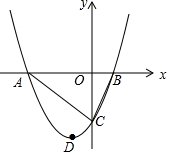 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c与x轴相交于点A(-3,0)和点B(1,0),与y轴相交于点C(0,-3),抛物线的顶点为点D,连接AC、BC.
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c与x轴相交于点A(-3,0)和点B(1,0),与y轴相交于点C(0,-3),抛物线的顶点为点D,连接AC、BC. 将一副三角尺按如图所示的方式叠放(两条直角边重合),则∠α的度数是75°.
将一副三角尺按如图所示的方式叠放(两条直角边重合),则∠α的度数是75°.