题目内容
15.已知AB是⊙O的直径,AB=2,AC和AD是⊙O的两条弦,AC=$\sqrt{2}$,AD=$\sqrt{3}$,求∠CAD的度数.分析 本题大致的思路是连接BC、BD,分别在Rt△CAB和Rt△BAD中,求出∠CAD和∠CAB的度数,然后根据D点的不同位置分类讨论.
解答 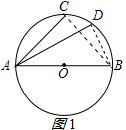 解:本题分两种情况:
解:本题分两种情况:
①当AD在AB上方时,如图1所示:
连接BD、BC,
则∠ADB=∠ACB=90°,
Rt△ACB中,AD=$\sqrt{3}$,AB=2,
∴∠DAB=30°,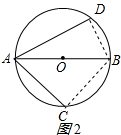 Rt△ACB中,AC=$\sqrt{2}$,AB=2,
Rt△ACB中,AC=$\sqrt{2}$,AB=2,
∴∠CAB=45°,
∴∠CAD=∠CAB-∠DAB=15°,
②当AD在AB下方时,如图2所示:
同①可求得∠CAD=75°.
故答案为:15°或75°.
点评 本题考查的是圆周角定理及直角三角形的性质,比较简单,但在解答时要注意分两种情况讨论,不要漏解,难度适中.

练习册系列答案
相关题目
20. 如图,点O是直线AB上一点,若∠1=35°,则∠2的度数为( )
如图,点O是直线AB上一点,若∠1=35°,则∠2的度数为( )
 如图,点O是直线AB上一点,若∠1=35°,则∠2的度数为( )
如图,点O是直线AB上一点,若∠1=35°,则∠2的度数为( )| A. | 125° | B. | 135° | C. | 145° | D. | 155° |
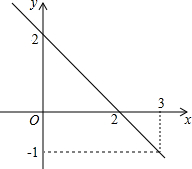 如图所示是一次函数y=kx+b的图象,则这个函数的表达式为y=-x+2.
如图所示是一次函数y=kx+b的图象,则这个函数的表达式为y=-x+2. 如图,在一长方形休闲广场的四角都设计一块半径相同的四分之一圆的花坛,若圆形的半径为r米,广场长为m米,宽为n米
如图,在一长方形休闲广场的四角都设计一块半径相同的四分之一圆的花坛,若圆形的半径为r米,广场长为m米,宽为n米