题目内容
某同学判断关于x的方程x2+2(k-2)x+k2+4=0的根的情况如下:
解:b2-4ac=4(k-2)2-4×1×(k2+4)①
=-16k.②
∵-16k<0,③
∴b2-4ab<0.④
∴原方程无实数根.⑤
请你判断该同学的解答是否正确,并写出你的判断理由.
解:b2-4ac=4(k-2)2-4×1×(k2+4)①
=-16k.②
∵-16k<0,③
∴b2-4ab<0.④
∴原方程无实数根.⑤
请你判断该同学的解答是否正确,并写出你的判断理由.
考点:根的判别式
专题:
分析:在进行判定-16k的取值时,出现错误,应当分三种情况探讨-16k的取值范围得出方程根的情况.
解答:解:不正确;
理由:
当k>0时,-16k<0,原方程无实数根.
当k=0时,-16k=0,原方程有两个相等的实数根.
当k<0时,-16k>0,原方程有两个不相等的实数根.
理由:
当k>0时,-16k<0,原方程无实数根.
当k=0时,-16k=0,原方程有两个相等的实数根.
当k<0时,-16k>0,原方程有两个不相等的实数根.
点评:此题考查根据根的判别式判别一元二次方程根的情况:若b2-4ac>0,则有两不相等的实数根;若b2-4ac<0,则无实数根;若b2-4ac=0,则有两相等的实数根.

练习册系列答案
相关题目
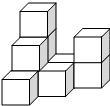 如图,在平整的地面上,有若干个完全相同的棱长为10cm的小正方体堆成一个几何体.
如图,在平整的地面上,有若干个完全相同的棱长为10cm的小正方体堆成一个几何体. 如图,两条直线a,b相交.
如图,两条直线a,b相交.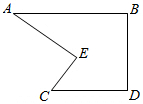 小明到工厂去进行社会实践活动时,发现工厂生产了一种如图所示的零件,工人师傅告诉他:AB∥CD,∠A=40°,∠AEC=70°,小明马上运用已学的数学知识得出了∠C的度数,聪明的你一定知道∠C的度数.
小明到工厂去进行社会实践活动时,发现工厂生产了一种如图所示的零件,工人师傅告诉他:AB∥CD,∠A=40°,∠AEC=70°,小明马上运用已学的数学知识得出了∠C的度数,聪明的你一定知道∠C的度数. 如图是一座人行天桥的示意图,天桥的高是10米,坡角是45°,为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面的倾斜角为30°,若新坡角需留3米的人行道,问:离原坡底A处11米的建筑物是否需要拆除?(
如图是一座人行天桥的示意图,天桥的高是10米,坡角是45°,为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面的倾斜角为30°,若新坡角需留3米的人行道,问:离原坡底A处11米的建筑物是否需要拆除?( 如图,△ABC中,DE垂直平分线段AB,AE=5cm,△ACD的周长为17cm,则△ABC的周长为
如图,△ABC中,DE垂直平分线段AB,AE=5cm,△ACD的周长为17cm,则△ABC的周长为