题目内容
18.不等式组$\left\{\begin{array}{l}{x-2>0}\\{x-a>0}\end{array}\right.$的解集为x>2,则a的取值范围是a≤2.分析 首先解每个不等式,然后根据不等式组的解集是x>2即可求解.
解答 解:$\left\{\begin{array}{l}{x-2>0…①}\\{x-a>0…②}\end{array}\right.$,
解①得x>2,
解②得x>a,
∵不等式组的解集是x>2,
∴a≤2.
故答案是:a≤2.
点评 本题考查了一元一次不等式组的解法:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
8.已知三角形三边长分别为5,x,17,若x为正整数,则这样的三角形个数为( )
| A. | 5个 | B. | 8个 | C. | 9个 | D. | 19个 |
9.下列各命题都成立,其中逆命题也成立的是( )
| A. | 若a>0,b>0,则a+b>0 | B. | 对顶角相等 | ||
| C. | 全等三角形的对应角相等 | D. | 平行四边形的两组对边分别相等 |
13.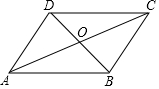 如图,已知AC、BD相交于点O,AO=CO,BO=DO,则图中能判定全等的三角形有( )
如图,已知AC、BD相交于点O,AO=CO,BO=DO,则图中能判定全等的三角形有( )
 如图,已知AC、BD相交于点O,AO=CO,BO=DO,则图中能判定全等的三角形有( )
如图,已知AC、BD相交于点O,AO=CO,BO=DO,则图中能判定全等的三角形有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
10.如果3xm+2y3与-2x3y2n-1是同类项,则m、n的值分别是( )
| A. | m=1,n=2 | B. | m=0,n=2 | C. | m=2,n=1 | D. | m=1,n=1 |
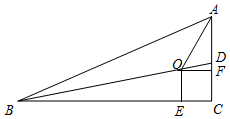 如图,在Rt△ABC中,∠C=90°,BD是Rt△ABC的一条角平分线,点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形(四边相等,四个角都是直角),
如图,在Rt△ABC中,∠C=90°,BD是Rt△ABC的一条角平分线,点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形(四边相等,四个角都是直角),