Question

【题目】如图，以△ABC的边AB为直径的⊙O分别交BC、AC于F、G，且G是的中点，过点G作DE⊥BC，垂足为E，交BA的延长线于点D

（1）求证：DE是的⊙O切线；

（2）若AB=6，BG=4，求BE的长；

（3）若AB=6，CE=1.2，请直接写出AD的长．

Answer 1

【答案】（1）证明见解析；（2）；（3）2.

【解析】

（1）要证明DE是的⊙O切线，证明OG⊥DE即可；

（2）先证明△GBA∽△EBG，即可得出=,根据已知条件即可求出BE；

（3）先证明△AGB≌△CGB，得出BC=AB=6，BE=4.8再根据OG∥BE得出=，即可计算出AD.

证明：（1）如图，连接OG，GB，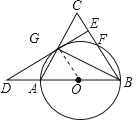

∵G是弧AF的中点，

∴∠GBF=∠GBA，

∵OB=OG，

∴∠OBG=∠OGB，

∴∠GBF=∠OGB，

∴OG∥BC，

∴∠OGD=∠GEB，

∵DE⊥CB，

∴∠GEB=90°，

∴∠OGD=90°，

即OG⊥DE且G为半径外端，

∴DE为⊙O切线；

（2）∵AB为⊙O直径，

∴∠AGB=90°，

∴∠AGB=∠GEB，且∠GBA=∠GBE，

∴△GBA∽△EBG，

∴，

∴；

（3）AD=2，根据SAS可知△AGB≌△CGB，

则BC=AB=6，

∴BE=4.8，

∵OG∥BE，

∴，即，

解得：AD=2．