题目内容
16.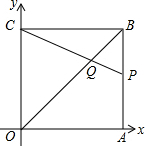 如图,正方形OABC的边长为6,顶点A,C在坐标轴上,点P在AB上,CP交OB于点Q,S△BPQ=$\frac{1}{4}$S△OQC,则点Q的坐标为(4,4).
如图,正方形OABC的边长为6,顶点A,C在坐标轴上,点P在AB上,CP交OB于点Q,S△BPQ=$\frac{1}{4}$S△OQC,则点Q的坐标为(4,4).
分析 过Q作EF⊥OC,垂足为E,交AB于点F,易证△OCQ∽△BPQ,由S△BPQ=$\frac{1}{4}$S△OQC,可知QF:QE=1:2,于是QE=4,可求出Q的坐标.
解答 解:过Q作EF⊥OC,垂足为E,交AB于点F,
∵四边形OABC是正方形,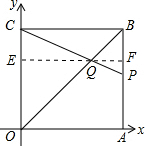
∴OC∥AB,
∴△OCQ∽△BPQ,
∵S△BPQ=$\frac{1}{4}$S△OQC,
∴$\frac{QF}{QE}=\frac{BP}{OC}=\frac{1}{2}$,
∵EF=BC=6.
∴QE=4,
∴Q的坐标(4,4).
故答案为:(4,4).
点评 本题主要考查了正方形的性质、相似三角形的判定与性质,熟知相似三角形的面积比等于相似比的平方是解决问题的关键.

练习册系列答案
相关题目
1.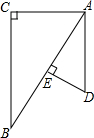 如图,已知△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,那么添加下列一个条件后,仍无法判定△ABC∽△DAE的是( )
如图,已知△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,那么添加下列一个条件后,仍无法判定△ABC∽△DAE的是( )
 如图,已知△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,那么添加下列一个条件后,仍无法判定△ABC∽△DAE的是( )
如图,已知△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,那么添加下列一个条件后,仍无法判定△ABC∽△DAE的是( )| A. | $\frac{AC}{DE}$=$\frac{AB}{AD}$ | B. | ∠B=∠D | C. | AD∥BC | D. | ∠BAC=∠D |
5.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  等边三角形 | B. |  平行四边形 | C. |  矩形 | D. |  正五边形 |
6.下列根式中能与$\sqrt{3}$合并的是( )
| A. | $\sqrt{6}$ | B. | $\sqrt{9}$ | C. | $\sqrt{12}$ | D. | $\sqrt{18}$ |
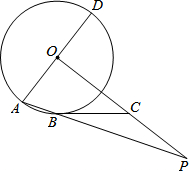 如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P.点C在OP上,且BC=PC.
如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P.点C在OP上,且BC=PC.