题目内容
如图所示，若⊙O 的半径为13cm，点P是弦AB上一动点，且到圆心的最短距离为5cm，则弦AB的长为分析：过O点作OC⊥AB于C，连OA，根据垂线段最短得到OC=5cm，根据垂径定理得到AC=BC，再利用勾股定理计算出AC，即可得到AB．
解答：
解：过O点作OC⊥AB于C，连OA，如图，
∴OC=5cm，AC=BC，
在Rt△OAC中，OA=13cm，
∴AC=
=
=12（cm），
∴AB=2AC=24cm．
故答案为：24cm．
解：过O点作OC⊥AB于C，连OA，如图，∴OC=5cm，AC=BC，
在Rt△OAC中，OA=13cm，
∴AC=
| OA2-OC2 |
| 132-52 |
∴AB=2AC=24cm．
故答案为：24cm．
点评：本题考查了垂径定理：垂直于弦的直径平分弦，并且平分弦所对的弧．也考查了勾股定理．
练习册系列答案
相关题目
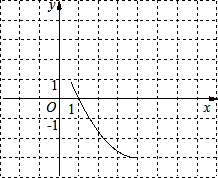已知抛物线y=| 1 |
| 3 |
| A、（5，0） |
| B、（6，0） |
| C、（7，0） |
| D、（0，7） |
二次函数y=-mx2+2mx+k的部分图象如图所示，若关于x的一元二次方程-mx2+2mx+k=0的一个解为x1=3，则另一个解x2=
2002年国际数学大会的会标如图所示，若大正方形的面积为13，每个直角三角形两直角边的和是5，则中间小正方形的面积为