题目内容
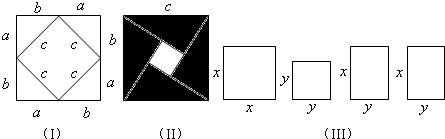
 2002年国际数学大会的会标如图所示,若大正方形的面积为13,每个直角三角形两直角边的和是5,则中间小正方形的面积为
2002年国际数学大会的会标如图所示,若大正方形的面积为13,每个直角三角形两直角边的和是5,则中间小正方形的面积为1
1
.分析:设直角三角形斜边为c,两直角边分别为a与b,利用勾股定理得到c2=a2+b2,再由大正方形的面积为13,每个直角三角形两直角边的和是5,得到c2=13,a+b=5,利用完全平方公式得到(a+b)2=a2+b2+2ab,将a+b,a2+b2=c2及c2=的值代入,求出2ab的值,中间小正方形的边长为直角三角形长直角边与短直角边之差,面积即为(b-a)2,利用完全平方公式展开后,将各自的值代入即可求出值.
解答:解:设每个直角三角形的斜边为c,直角边分别为a,b,则有c2=a2+b2,
∵c2=13,a+b=5,
∴(a+b)2=a2+b2+2ab=c2+2ab=13+2ab=25,即2ab=12,
则中间小正方形的面积为(b-a)2=a2+b2-2ab=c2-2ab=13-12=1.
故答案为:1
∵c2=13,a+b=5,
∴(a+b)2=a2+b2+2ab=c2+2ab=13+2ab=25,即2ab=12,
则中间小正方形的面积为(b-a)2=a2+b2-2ab=c2-2ab=13-12=1.
故答案为:1
点评:此题考查了勾股定理,以及完全平方公式的运用,其中根据题意得出中间小正方形的边长为直角三角形长直角边与短直角边之差是解本题的关键.

练习册系列答案
相关题目

 ab,即(a+b)2=c2+4×
ab,即(a+b)2=c2+4×