题目内容
 【问题发现】
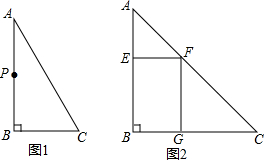
【问题发现】(1)如图①,△ABC为直角三角形,∠B=90°,P是边AB上任意一点(不写A、B重合),请你在△ABC的边长找另一点Q,使得S△BCP=S△BCQ,并简要说明方法;
(2)如图②,△ABC为等腰三角形,∠B=90°,AB=10,F是边AC上任意一点(不与A、C重合),EF⊥AB,FG⊥BC,试判断图中△AEF、△CGF、四边形BEFG的具体形状;(直接写出答案).
【问题探究】
(3)在(2)的条件下研究:F在边长AC上移动时,四边形BEFG的周长是否发生改变,并说明理由;(不妨设AE=x)
(4)在(2)的条件下研究:F在边AC上移动时,四边形BEFG的面积是否存在最大值?若存在,求出来;若不存在,说明理由.(提示:我们知道完全平方式具有非负性,即(a+b)2≥0,显然(a+b)2有最小值.例如:对于y=x2+2x+2=(x+1)2+1≥1,那么y有最小值1).
考点:相似形综合题
专题:
分析:(1)过点P作PQ∥BC,交AC于Q,连接PQ即可;
(2)根据EF⊥AB,FG⊥BC,∠B=90°,可直接得出四边形BEFG是长方形;
(3)先求出AE=EF,再根据四边形BEFG的周长=2(EF+BE)=2(AE+BE)=2AB得出四边形BEFG的周长总是20,不会发生改变;
(4)设AE=x(0<x<10),则BE=10-x,EF=x,得出S长方形BEFG=BE•EF=-(x-5)2+25,从而得出当x=5时,有最大值25.
(2)根据EF⊥AB,FG⊥BC,∠B=90°,可直接得出四边形BEFG是长方形;
(3)先求出AE=EF,再根据四边形BEFG的周长=2(EF+BE)=2(AE+BE)=2AB得出四边形BEFG的周长总是20,不会发生改变;
(4)设AE=x(0<x<10),则BE=10-x,EF=x,得出S长方形BEFG=BE•EF=-(x-5)2+25,从而得出当x=5时,有最大值25.
解答: 解:(1)过点P作PQ∥BC,交AC于Q,连接PQ,
解:(1)过点P作PQ∥BC,交AC于Q,连接PQ,
∵PQ∥BC,
∴△BCQ和△BCP同底等高,
∴S△BCP=S△BCQ;
(2)∵EF⊥AB,FG⊥BC
∴∠BEF=90°,∠BGF=90°,
∵∠B=90°,
∴四边形BEFG是长方形;
(3)F在边长AC上移动时,四边形BEFG的周长不会发生改变.理由如下:
∵∠B=90°,AB=BC,
∴∠A=∠C=45°,
∵EF⊥AB,
∴∠A=∠AFE=45°,
∴AE=EF,
∴四边形BEFG的周长=2(EF+BE)=2(AE+BE)=2AB=2×10=20,
∴F在边长AC上移动时,四边形BEFG的周长总是20,不会发生改变;
(4)由(3)可得知:AE=EF,AB=10
设AE=x(0<x<10),则BE=10-x,EF=x
∵S长方形BEFG=BE•EF=x(10-x)=10x-x2=-(x-5)2+25,
∴当x=5时,有最大值,
S最大值=25
答:F在边AC上移动时,四边形BEFG的面积有最大值,最大值是25.
 解:(1)过点P作PQ∥BC,交AC于Q,连接PQ,
解:(1)过点P作PQ∥BC,交AC于Q,连接PQ,∵PQ∥BC,
∴△BCQ和△BCP同底等高,
∴S△BCP=S△BCQ;
(2)∵EF⊥AB,FG⊥BC
∴∠BEF=90°,∠BGF=90°,
∵∠B=90°,
∴四边形BEFG是长方形;
(3)F在边长AC上移动时,四边形BEFG的周长不会发生改变.理由如下:
∵∠B=90°,AB=BC,
∴∠A=∠C=45°,
∵EF⊥AB,
∴∠A=∠AFE=45°,
∴AE=EF,
∴四边形BEFG的周长=2(EF+BE)=2(AE+BE)=2AB=2×10=20,
∴F在边长AC上移动时,四边形BEFG的周长总是20,不会发生改变;
(4)由(3)可得知:AE=EF,AB=10
设AE=x(0<x<10),则BE=10-x,EF=x
∵S长方形BEFG=BE•EF=x(10-x)=10x-x2=-(x-5)2+25,
∴当x=5时,有最大值,
S最大值=25
答:F在边AC上移动时,四边形BEFG的面积有最大值,最大值是25.
点评:此题考查了相似形综合,用到的知识点是三角形的面积、二次函数的最值、矩形的判定与面积、等腰直角三角形,关键是根据题意画出图形,列出表示长方形面积的式子.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
将△ABC向左平移2个单位长度后得到△A′B′C′.若点A的坐标是(-3,7),则点A′的坐标是( )
| A、(-5,5) |
| B、(-1,9) |
| C、(-5,7) |
| D、(-1,7) |
将抛物线y=x2向左平移6个单位,再向下平移8个单位后的抛物线为( )
| A、y=(x+6)2-8 |
| B、y=(x-6)2+8 |
| C、y=(x-6)2-8 |
| D、y=(x+6)2+8 |
下列命题中,正确的是( )
①顶点在圆周上的角是圆周角;②90°的圆周角所对的弦是直径;③圆周角度数等于圆心角度数的一半;④三点确定一个圆;⑤同弧所对的圆周角相等.
①顶点在圆周上的角是圆周角;②90°的圆周角所对的弦是直径;③圆周角度数等于圆心角度数的一半;④三点确定一个圆;⑤同弧所对的圆周角相等.
| A、①②③ | B、③④⑤ |
| C、②⑤ | D、②③ |
在同一坐标系中,抛物线y=x2,y=-x2,y=
x2的共同点是( )
| 1 |
| 2 |
| A、开口向上,对称轴是y轴,顶点是原点 |
| B、对称轴是y轴,顶点是原点 |
| C、开口向下,对称轴是y轴,顶点是原点 |
| D、有最小值为0 |
下列函数中是二次函数的为( )
| A、y=3x-1 |
| B、y=3x2-1 |
| C、y=(x+1)2-x2 |
| D、y=x3+2x-3 |
在下列函数中,属于二次函数的是( )
A、y=
| ||
B、y=x2+
| ||
| C、y=2x2-1 | ||
D、y=
|