题目内容
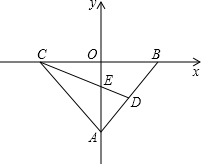 如图所示,在直角坐标系xOy中,点A在y轴负半轴上,点B、C分别在x轴正、负半轴上,AO=8,AB=AC,sin∠ABC=
如图所示,在直角坐标系xOy中,点A在y轴负半轴上,点B、C分别在x轴正、负半轴上,AO=8,AB=AC,sin∠ABC=| 4 |
| 5 |
考点:二次函数综合题
专题:计算题,数形结合,转化思想
分析:已知AB=AC,显然有OB=OC,因此只需求出点B的坐标即可确定点C的坐标;在Rt△ABC中,已知AO、∠ABC的正弦值即可求出OB的长,可据此求出点B、C的坐标.
求点E的坐标时,要把握住S△COE=S△ADE这个条件,由图可看出这两个三角形的面积不好得出,因此让它们加上一个公共图形,转化为S△CDB=S△AOB更方便求解,先求出点D的坐标,进一步可求出点E的坐标,再由待定系数法即可确定抛物线的解析式.
求点E的坐标时,要把握住S△COE=S△ADE这个条件,由图可看出这两个三角形的面积不好得出,因此让它们加上一个公共图形,转化为S△CDB=S△AOB更方便求解,先求出点D的坐标,进一步可求出点E的坐标,再由待定系数法即可确定抛物线的解析式.
解答: 解:因为sin∠ABC=
解:因为sin∠ABC=
=
,AO=8,
所以AB=10.由勾股定理,得BO=
=6.
易知△ABO≌△ACO,因此 CO=BO=6.
于是A(0,-8),B(6,0),C(-6,0).
设点D的坐标为(m,n).
由S△COE=S△ADE,得S△CDB=S△AOB.所以
BC•|n|=
AO•BO,
×12(-n)=
×8×6.
解得 n=-4.
因此D为AB的中点,点 D的坐标为(3,-4).
因此CD,AO分别为AB,BC的两条中线,点E为△ABC的重心,
所以点E的坐标为(0,-
).(也可由直线CD交y轴于点E来求得.)
设经过B,C,E三点的二次函数的解析式为y=a(x-6)(x+6).
将点E的坐标代入,解得a=
.
故经过B,C,E三点的二次函数的解析式为y=
x2-
.
 解:因为sin∠ABC=
解:因为sin∠ABC=| AO |
| AB |
| 4 |
| 5 |
所以AB=10.由勾股定理,得BO=
| AB2-AO2 |
易知△ABO≌△ACO,因此 CO=BO=6.
于是A(0,-8),B(6,0),C(-6,0).
设点D的坐标为(m,n).
由S△COE=S△ADE,得S△CDB=S△AOB.所以
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得 n=-4.
因此D为AB的中点,点 D的坐标为(3,-4).
因此CD,AO分别为AB,BC的两条中线,点E为△ABC的重心,
所以点E的坐标为(0,-
| 8 |
| 3 |
设经过B,C,E三点的二次函数的解析式为y=a(x-6)(x+6).
将点E的坐标代入,解得a=
| 2 |
| 27 |
故经过B,C,E三点的二次函数的解析式为y=
| 2 |
| 27 |
| 8 |
| 3 |
点评:该题主要考查的是利用待定系数法确定二次函数的解析式,其中求点E的坐标是本题的难点,解题时要注意转化思想的合理应用,例如:将S△COE=S△ADE转化为S△CDB=S△AOB后,可大大降低解题的难度.

练习册系列答案
相关题目
下列调查中,适宜采用普查方式的是( )
| A、调查全国中学生的视力情况 |
| B、调查重庆新闻节目”天天630”的收视率 |
| C、调查“神九”航天飞船各零部件的质量 |
| D、调查重庆市民对生活质量的满意程度 |
在实数0、-
、|-3|、-
中,最小的是( )
| 2 |
| 2 |
| 3 |
| A、0 | ||
B、-
| ||
| C、|-3| | ||
D、-
|
 如图,AD是△ABC的中线,E是AD上的一点,且AE=
如图,AD是△ABC的中线,E是AD上的一点,且AE=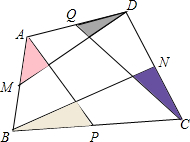 如图,在四边形ABCD中,M为AB的中点,P为BC的中点,N为CD的中点,Q为DA的中点,若图中中间的小四边形的面积为1,试求四个小三角形(阴影部分)面积之和.
如图,在四边形ABCD中,M为AB的中点,P为BC的中点,N为CD的中点,Q为DA的中点,若图中中间的小四边形的面积为1,试求四个小三角形(阴影部分)面积之和.