题目内容
4. 如图,A、B、C分别是线段A1B,B1C,C1A的中点,若△A1B1C1的面积是a,那么△ABC的面积是$\frac{a}{7}$.(用a的代数式表示)
如图,A、B、C分别是线段A1B,B1C,C1A的中点,若△A1B1C1的面积是a,那么△ABC的面积是$\frac{a}{7}$.(用a的代数式表示)
分析 连接AB1,BC1,CA1,根据等底等高的三角形的面积相等求出△ABB1,△A1AB1的面积,从而求出△A1BB1的面积,同理可求△B1CC1的面积,△A1AC1的面积,于是得到结论.
解答  解:如图,连接AB1,BC1,CA1,
解:如图,连接AB1,BC1,CA1,
∵A、B分别是线段A1B,B1C的中点,
∴S△ABB1=S△ABC,
S△A1AB1=S△ABB1=S△ABC,
∴S△A1BB1=S△A1AB1+S△ABB1=2S△ABC,
同理:S△B1CC1=2S△ABC,S△A1AC1=2S△ABC,
∴△A1B1C1的面积=S△A1BB1+S△B1CC1+S△A1AC1+S△ABC=7S△ABC=a.
∴S△ABC=$\frac{a}{7}$,
故答案为:$\frac{a}{7}$.
点评 本题考查了三角形的面积,主要利用了等底等高的三角形的面积相等,作辅助线把三角形进行分割是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
15.某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方体形状的无盖纸盒.
(1)现有正方形纸板162张,长方形纸板340张.若要做两种纸盒共100个,设做竖式纸盒x个.
①根据题意,完成以下表格:
②按两种纸盒的生产个数来分,有哪几种生产方案?
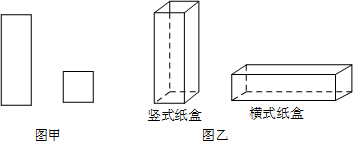
(1)现有正方形纸板162张,长方形纸板340张.若要做两种纸盒共100个,设做竖式纸盒x个.
①根据题意,完成以下表格:
| 竖式纸盒(个) | 横式纸盒(个) | |
| 正方形纸板(张) | x | 2(100-x) |
| 长方形纸板(张) | 4x | 3(100-x) |

12. 如图:有一块含有45°的直角三角板的两个顶点放在直尺的对边上,如果∠1=20°,那么∠2的度数是( )
如图:有一块含有45°的直角三角板的两个顶点放在直尺的对边上,如果∠1=20°,那么∠2的度数是( )
 如图:有一块含有45°的直角三角板的两个顶点放在直尺的对边上,如果∠1=20°,那么∠2的度数是( )
如图:有一块含有45°的直角三角板的两个顶点放在直尺的对边上,如果∠1=20°,那么∠2的度数是( )| A. | 30° | B. | 25° | C. | 20° | D. | 15° |
19.把矩形纸片对折两次,在顶端处剪掉一个小三角形,展开纸片,纸片上留下一个孔,这个孔的形状是( )
| A. | 等腰三角形 | B. | 菱形 | C. | 矩形 | D. | 平行四边形 |
13.下列命题中,属于真命题的是( )
| A. | 两个锐角的和是锐角 | B. | 在同一平面内,如果a⊥b,b⊥c,则a⊥c | ||
| C. | 同位角相等 | D. | 在同一平面内,如果a∥b,b∥c,则a∥c |
 如图所示,转盘被等分成六个扇形,并在上面依次写上数字1、2、3、4、5、6.
如图所示,转盘被等分成六个扇形,并在上面依次写上数字1、2、3、4、5、6. 如图,在△ABC中,D、E分别是AC、AB边上的点,若要△ADE与△ABC相似,则需要添加的一个条件是∠ADE=∠B.
如图,在△ABC中,D、E分别是AC、AB边上的点,若要△ADE与△ABC相似,则需要添加的一个条件是∠ADE=∠B.