题目内容
5. 如图,点D,E分别在AB,AC上,如果△ABC与△AED相似,若DE=3,AB=10,AC=7,BC=6,则AD的长为5或3.5.
如图,点D,E分别在AB,AC上,如果△ABC与△AED相似,若DE=3,AB=10,AC=7,BC=6,则AD的长为5或3.5.
分析 分①AD与AB是对应边时,△ABC∽△ADE,利用相似三角形对应边成比例列式计算即可得解,②AD与AC是对应边时,△ABC∽△AED,利用相似三角形对应边成比例列式计算即可得解.
解答 解:①AD与AB是对应边时,△ABC∽△ADE,
则$\frac{AD}{AB}$=$\frac{DE}{BC}$,
即$\frac{AD}{10}$=$\frac{3}{6}$,
解得AD=5,
②AD与AC是对应边时,△ABC∽△AED,
则$\frac{AD}{AC}$=$\frac{DE}{BC}$,
即$\frac{AD}{7}$=$\frac{3}{6}$,
解得AD=3.5,
综上所述,AD的长为5或3.5.
故答案为:5或3.5.
点评 本题考查了相似三角形的性质,主要利用了相似三角形对应边成比例,难点在于分情况讨论.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
13.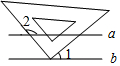 如图,已知a∥b,小亮把三角板的直角顶点放在直线a上,若∠1=40°,则∠2的度数为( )
如图,已知a∥b,小亮把三角板的直角顶点放在直线a上,若∠1=40°,则∠2的度数为( )
 如图,已知a∥b,小亮把三角板的直角顶点放在直线a上,若∠1=40°,则∠2的度数为( )
如图,已知a∥b,小亮把三角板的直角顶点放在直线a上,若∠1=40°,则∠2的度数为( )| A. | 160° | B. | 140° | C. | 130° | D. | 50° |
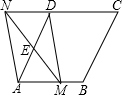 如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.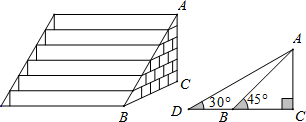
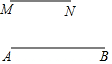 如图,已知线段AB=a,MN=b,按照下列要求画(作)图与计算.
如图,已知线段AB=a,MN=b,按照下列要求画(作)图与计算. 如图,在?ABCD中,∠ABC的平分线BF分别与AC、AD交于点E、F.
如图,在?ABCD中,∠ABC的平分线BF分别与AC、AD交于点E、F. 如图,AM∥BN,AC⊥BC,如果∠A-∠B=10°,那么∠A的度数是50°.
如图,AM∥BN,AC⊥BC,如果∠A-∠B=10°,那么∠A的度数是50°.