Question

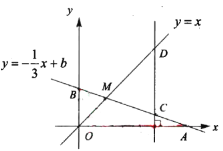
【题目】如图，函数的图像与轴、轴分别交于点、，与函数的图像交于点，点的横坐标为．

（1）求点的坐标；

（2）在轴上有一动点．

①若三角形是以为底边的等腰三角形，求的值；

②过点作轴的垂线，分别交函数和的图像于点、，若，求的值．

Answer 1

【答案】（1）A(12,0)；（2）a=；（3）a=6.

【解析】

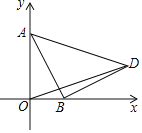
（1）先根据点M在直线y=x上求出M（3，3），把M（3，3）代入可计算出b=4，得到一次函数的解析式为，然后根据x轴上点的坐标特征可确定A点坐标为（12，0）；

（2）①分别求出PB和PA的长，根据PA=PB列出方程，求出a的值即可；

②先表示出C（a，），D（a，a），根据CD=2CP列方程求解即可.

（1）∵点的横坐标为，且点M在直线y=x上，

∴点M的横坐标为3，

∴M（3，3）

把M（3，3）代入得，，解得，b=4，

∴，

当y=0时，x=12，

∴A(12，0)，

（2）①对于，当x=0时，y=4，

∴B(0，4)，

∵P（a，0），

∴PO=a，AP=12-a，

在Rt△BPO中，

∴

∵PA=PB，

∴，

解得，a=；

②∵P（a，0），

∴C（a，），D（a，a）

∴PC=，PD=a，

∴DC=PD-PC=，

∵，

∴=2（），

解得：a=6.