题目内容
14.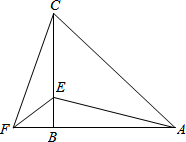 如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.求证:BE=BF.
如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.求证:BE=BF.
分析 根据“HL”判断Rt△ABE≌Rt△CBF,则可得到BE=BF.
解答 证明:如图,∵∠ABC=90°,
∴∠CBF=90°
在Rt△ABE和Rt△CBF中,
$\left\{\begin{array}{l}{AB=BC}\\{AE=CF}\end{array}\right.$,
∴Rt△ABE≌Rt△CBF(HL),
∴BE=BF.
点评 此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
2.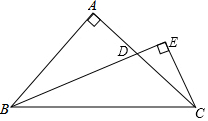 已知等腰直角三角形ABC,BC是斜边,∠B的平分线交AC于D,过C作CE与BD垂直且交BD延长线于E.已知CE=4,则BD的长为( )
已知等腰直角三角形ABC,BC是斜边,∠B的平分线交AC于D,过C作CE与BD垂直且交BD延长线于E.已知CE=4,则BD的长为( )
 已知等腰直角三角形ABC,BC是斜边,∠B的平分线交AC于D,过C作CE与BD垂直且交BD延长线于E.已知CE=4,则BD的长为( )
已知等腰直角三角形ABC,BC是斜边,∠B的平分线交AC于D,过C作CE与BD垂直且交BD延长线于E.已知CE=4,则BD的长为( )| A. | 5 | B. | 8 | C. | $\sqrt{73}$ | D. | 7 |
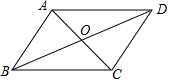 要做一个平行四边形框架,只要将两根木条AC、BD的中点重叠并用钉子固定,这样四边形ABCD就是平行四边形,这种做法的依据是两条对角线分别平分的四边形是平行四边形.
要做一个平行四边形框架,只要将两根木条AC、BD的中点重叠并用钉子固定,这样四边形ABCD就是平行四边形,这种做法的依据是两条对角线分别平分的四边形是平行四边形.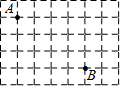 如图,长方形网格由小正方形构成,每一个小正方形的边长都为1,点A和点B是小正方形的格点,请你在图中画出从A到B的最短路程,则点A和点B之间的这个最短路程值为5.
如图,长方形网格由小正方形构成,每一个小正方形的边长都为1,点A和点B是小正方形的格点,请你在图中画出从A到B的最短路程,则点A和点B之间的这个最短路程值为5.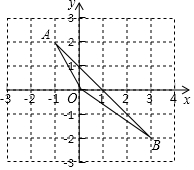 已知:点A、B在平面直角坐标系中的位置如图所示,
已知:点A、B在平面直角坐标系中的位置如图所示,