题目内容
△ABC为⊙O的内接三角形，若∠AOC=160°，则∠ABC的度数是
- A.80°
- B.160°
- C.100°
- D.80°或100°
D
分析：首先根据题意画出图形，由圆周角定理即可求得答案∠ABC的度数，又由圆的内接四边形的性质，即可求得∠AB′C的度数．
解答：
解：如图，∵∠AOC=160°，
∴∠ABC=
∠AOC=×160°=80°，
∵∠ABC+∠AB′C=180°，
∴∠AB′C=180°-∠ABC=180°-80°=100°．
∴∠ABC的度数是：80°或100°．
故选D．
点评：此题考查了圆周角定理与圆的内接四边形的性质．此题难度不大，注意数形结合思想与分类讨论思想的应用，注意别漏解．
分析：首先根据题意画出图形，由圆周角定理即可求得答案∠ABC的度数，又由圆的内接四边形的性质，即可求得∠AB′C的度数．
解答：
解：如图，∵∠AOC=160°，∴∠ABC=
∠AOC=×160°=80°，∵∠ABC+∠AB′C=180°，
∴∠AB′C=180°-∠ABC=180°-80°=100°．
∴∠ABC的度数是：80°或100°．
故选D．
点评：此题考查了圆周角定理与圆的内接四边形的性质．此题难度不大，注意数形结合思想与分类讨论思想的应用，注意别漏解．
练习册系列答案
相关题目
5、如图，△ABC为⊙O的内接三角形，AB是直径，∠A=20°，则∠B的度数是（ ）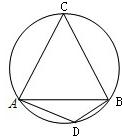
于点D、E．
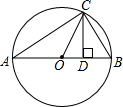探究证明：