题目内容
15、如图，△ABC为⊙O的内接正三角形，D为⊙O上一点，则∠ADB=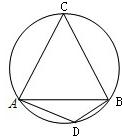
120
度．分析：由于△ABC为⊙O的内接正三角形，所以∠C=60°，又因为四边形ACBD是圆的内接四边形，所以∠C+∠ADB=180°，所以
∠ADB=120°．
∠ADB=120°．
解答：解：∵△ABC为⊙O的内接正三角形，
∴∠C=60°，
又∵四边形ACBD是圆的内接四边形，
∴∠C+∠ADB=180°，
∴∠ADB=180°-60°=120°．
∴∠C=60°，
又∵四边形ACBD是圆的内接四边形，
∴∠C+∠ADB=180°，
∴∠ADB=180°-60°=120°．
点评：主要考查圆内接四边形的性质：圆内接四边形对角互补．题目典型，是一定基础题．
练习册系列答案
阅读快车系列答案
相关题目
种不同的平行四边形，并计算其中一种平行四边形的对角线的长．
5、如图，△ABC为⊙O的内接三角形，AB是直径，∠A=20°，则∠B的度数是（ ）
如图，△ABC为等边三角形，D、F分别为BC、AB上的点，且CD=BF，以AD为边作等边△ADE．
22、如图，△ABC为等边三角形，又DE⊥BC，EF⊥AC，FD⊥AB，垂足分别为E，F，D，则△DEF是等边三角形吗？说明你的理由．
23、如图，△ABC为等边三角形，D为BC上一点，∠ADE=60°，DE交∠ACB外角平分线于E．