题目内容
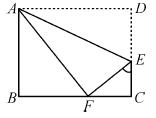
(12分)如图所示,E是正方形ABCD的边AB上的动点,正方形的边长为4, EF⊥DE交BC于点F.


(1)求证:△ADE ∽△BEF ;
(2)AE=x,BF=y.当x取什么值时,y有最大值? 并求出这个最大值;
(3)已知D、C 、F、E四点在同一个圆上,连接CE、DF,若sin∠CEF =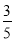 ,求此圆直径.
,求此圆直径.
(1)见解析;(2)当x=2时,y值最大,最大为1;(3)此圆直径为5.
【解析】
试题分析::(1)这两个三角形中,已知的条件有∠A=∠B=90°,那么只要得出另外两组对应角相等即可得出两三角形相似,因为∠DEA+∠FEB=180-90=90°,而∠ADE+∠DEA=90°,因此∠ADE=∠FEB,同理可得出∠BFE=∠AED,那么就构成了两三角形相似的条件;
(2)可用x表示出BE的长,然后根据(1)中三角形ADE和FEB相似可得出关于AD,AE,BE,BF的比例关系式,然后就能得出一个关于x,y的函数关系式.根据函数的性质即可得出y的最大值及相应的x的值.
(3)根据四点共圆,利用三角函数得出圆的直径.
试题解析:(1)证明:∵∠DEF=90°,
∴∠AED+∠BEF=90°,∠AED +∠ADE=90°,
∴∠ADE =∠BEF ,
∵∠A =∠B,
∴△ADE∽△BEF ;
(2)∵△ADE∽△BEF,
∴AD:BE=AE:BF,
∵AE=x,BF =y,AD =4,
∴4:x=(4-x):y,
∴y=-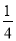 x2+x,
x2+x,
∴y=-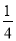 (x-2)2+1,
(x-2)2+1,
∴当x=2时,y值最大,最大为1;
∵D、C 、F、E四点共圆,
∴∠CEF=∠CDF,
∴sin∠CEF=sin∠CDF=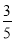 ,
,
∴DF=5,
即此圆直径为5
考点:正方形的性质;二次函数的最大值.

练习册系列答案
相关题目
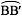 的长为( )
的长为( )
 B.
B.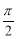 C.7
C.7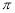 D.6
D.6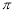
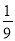 B.
B.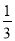 C.
C.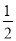 D.
D.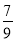



 = ;
= ;