题目内容
如图,∠AOB是直角,射线OC从OA出发,以每秒8度的速度顺时针方向转动;射线OD从OB出发,以每秒2度的速度逆时针方向转动.当OC与OA成一直线时停止转动.

(1)______秒时,OC与OD重合.
(2)当OC与OD的夹角是30度时,求转动的时间是多少秒?
(3)若OB平分∠COD,求转动的时间是多少秒?并画出此时的OC与OD,写出图中∠AOD的余角.
(1)9;(2)当转动6秒或12秒时,OC与OD的夹角是30度;
(3)转动15秒时,OB平分∠COD.
【解析】
试题分析:(1)利用两射线转动的速度和方向以及利用∠AOB是直角,得出等式求出即可;
(2)利用两射线转动的速度和方向以及利用∠AOB是直角,得出等式求出即可;
(3)利用OB平分∠COD,进而得出等式求出即可.
试题解析:
(1)∵∠AOB是直角,射线OC从OA出发,以每秒8度的速度顺时针方向转动;射线OD从OB出发,以每秒2度的速度逆时针方向转动,
∴设x秒时,OC与OD重合,则8x+2x=90,
解得:x=9,
故答案为:9;
(2)设转动t秒时,OC与OD的夹角是30度
根据题意,得:8t+2t=90-30或8t+2t=90+30
解之得t=6或t=12
答:当转动6秒或12秒时,OC与OD的夹角是30度.
设转动m秒时,OB平分∠COD
则:8m-90=2m
解之得:m=15
答:转动15秒时,OB平分∠COD
此时,OC和OD的位置如图

∠AOD的余角有∠BOD和∠BOC.
考点:一元一次方程的应用;角平分线的定义;余角和补角.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 ,则
,则 的值为
的值为 
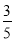 ,求此圆直径.
,求此圆直径. ,则边AC的长是 .
,则边AC的长是 . 的斜坡上两树间的水平距离AC为
的斜坡上两树间的水平距离AC为 ,则两树间的坡面距离AB为( ).
,则两树间的坡面距离AB为( ).
 B.
B. C.
C. D.
D.
 ,其中
,其中
 ,AC=4,BC=2,以AB为边向△ABC外作△ABD,使△ABD为等腰直角三角形,求线段CD的长.
,AC=4,BC=2,以AB为边向△ABC外作△ABD,使△ABD为等腰直角三角形,求线段CD的长.