题目内容
 如图,△ABC是等腰直角三角形,BD平分∠ABC,DE⊥BC于点E,且BC=10cm,则△DCE的周长为
如图,△ABC是等腰直角三角形,BD平分∠ABC,DE⊥BC于点E,且BC=10cm,则△DCE的周长为考点:角平分线的性质,等腰直角三角形
专题:
分析:根据等腰直角三角形和角平分线性质得出AD=DE,∠A=∠BED=90°,∠ABD=∠EBD,根据AAS证△ABD≌△EBD,推出AB=BE,求出△DCE的周长=DE+EC+CD=BC,即可得出答案.
解答:解:∵△ABC是等腰直角三角形,BD平分∠ABC,DE⊥BC,
∴AD=DE,∠A=∠BED=90°,∠ABD=∠EBD,
在△ABD和△EBD中
∴△ABD≌△EBD,
∴AB=BE,
∵AB=AC,
∴BE=AC,
∴△DCE的周长=DE+EC+CD=AD+EC+DC=AC+EC=BE+EC=BC=10cm,
故答案为:10.
∴AD=DE,∠A=∠BED=90°,∠ABD=∠EBD,
在△ABD和△EBD中
|
∴△ABD≌△EBD,
∴AB=BE,
∵AB=AC,
∴BE=AC,
∴△DCE的周长=DE+EC+CD=AD+EC+DC=AC+EC=BE+EC=BC=10cm,
故答案为:10.
点评:本题考查了全等三角形的性质和判定和角平分线性质的应用,解此题的关键是求出AD=DE,AC=BE,注意:角平分线上的点到角两边的距离相等.

练习册系列答案
相关题目
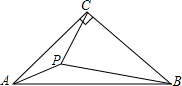 如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=1,PB=3,PC=2,则∠APC等于( )
如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=1,PB=3,PC=2,则∠APC等于( )| A、105° | B、120° |
| C、135° | D、150° |
实数a、b在数轴上的位置如图所示,那么化简|b-a|-
的结果是( )

| a2 |

| A、2a-b | B、b |
| C、-b | D、-2a+b |
已知两个相似多边形的相似比是3:4,其中较小多边形的周长为36cm,则较大多边形的周长为( )
| A、48cm | B、54cm |
| C、56cm | D、64cm |

 已知抛物线y=-x2+2x+3.
已知抛物线y=-x2+2x+3. 如图,一个水坝的截面是梯形,坝顶宽4m,坝高为6m,迎水坡的坡度为i=1:
如图,一个水坝的截面是梯形,坝顶宽4m,坝高为6m,迎水坡的坡度为i=1: