题目内容
16. 如图,在△ABC中.AB=AC,D为AB上的一点.DE∥AC交BC于E.△DBE是等腰三角形吗?为什么?
如图,在△ABC中.AB=AC,D为AB上的一点.DE∥AC交BC于E.△DBE是等腰三角形吗?为什么?
分析 由在△ABC中,AB=AC,由等边对等角,可得∠B=∠C,又由DE∥AC,利用平行线的性质,可得∠C=∠BED,继而可得∠BED=∠B,即可证得△DBE是等腰三角形.
解答 证明:∵AB=AC,
∴∠B=∠C,
∵ED∥AC,
∴∠C=∠BED,
∴∠B=∠BED,
∴ED=DB,
即△DBE是等腰三角形.
点评 此题考查了等腰三角形的性质与判定以及平行线的性质.此题比较简单,注意等边对等角与等角对等边定理的应用.

练习册系列答案
相关题目
4.下面图形是多边形的是( )
| A. |  | B. |  | C. |  | D. |  |
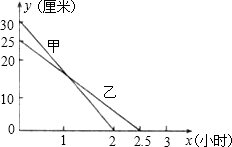 在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(时)之间的关系如图所示,请根据图象所提供的信息回答下列问题
在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(时)之间的关系如图所示,请根据图象所提供的信息回答下列问题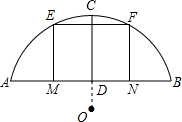 某桥主拱桥是圆弧形,跨度AB=60m.拱高CD=10m.
某桥主拱桥是圆弧形,跨度AB=60m.拱高CD=10m. 下图是五边形,它有五个内角,五条边,从一个顶点出发的对角线有2条.
下图是五边形,它有五个内角,五条边,从一个顶点出发的对角线有2条. 在图示的直角坐标系中分别作出y=-2x与y=-2x+3的图象,并说出两个图象之间的关系,以及各自函数图象的特点.
在图示的直角坐标系中分别作出y=-2x与y=-2x+3的图象,并说出两个图象之间的关系,以及各自函数图象的特点. 如图,AB是⊙O的直径,⊙O交BC于点D,DE⊥AC于点E,BD=CD.求证:DE是⊙O的切线.
如图,AB是⊙O的直径,⊙O交BC于点D,DE⊥AC于点E,BD=CD.求证:DE是⊙O的切线.