题目内容
17.先化简,再求值:($\frac{3x+4}{{x}^{2}-1}$-$\frac{2}{x-1}$)÷$\frac{{x}^{2}+2x}{{x}^{2}-1}$,其中x=$\sqrt{2}$.分析 先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:原式=[$\frac{3x+4}{(x+1)(x-1)}$-$\frac{2(x+1)}{(x+1)(x-1)}$]•$\frac{(x+1)(x-1)}{x(x+2)}$
=$\frac{3x+4-2x-2}{(x+1)(x-1)}$•$\frac{(x+1)(x-1)}{x(x+2)}$
=$\frac{x+2}{(x+1)(x-1)}$•$\frac{(x+1)(x-1)}{x(x+2)}$
=$\frac{1}{x}$,
当x=$\sqrt{2}$时,原式=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
7.下列各组线段,不能构成直角三角形的是( )
| A. | 3,4,5 | B. | 6,8,10 | C. | $\sqrt{3}$,2,$\sqrt{5}$ | D. | 5,12,13 |
8.下列等式中,计算正确的是( )
| A. | a2•a3=a6 | B. | (a2b3)m=(am)2•(bm)3 | C. | (am+bn)2=a2m+b2n | D. | a2+b3=2a5 |
6.若式子$\sqrt{4-3x}$在实数范围内有意义,则x的取值范围是( )
| A. | x>$\frac{4}{3}$ | B. | x<$\frac{4}{3}$ | C. | x≥$\frac{4}{3}$ | D. | x≤$\frac{4}{3}$ |
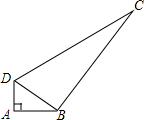 如图,在四边形ABCD中,∠BAD=90°,AD=1.5,AB=2,连接BD.
如图,在四边形ABCD中,∠BAD=90°,AD=1.5,AB=2,连接BD.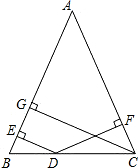 如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.
如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高. 如图所示,△ABC沿射线XY的方向平移一定距离后成为△DEF,找出图中存在的平行且相等的三条线段是AD∥CF,AD=CF=BE.
如图所示,△ABC沿射线XY的方向平移一定距离后成为△DEF,找出图中存在的平行且相等的三条线段是AD∥CF,AD=CF=BE.