题目内容
11．乘法公式的探究及应用．（1）如图1，若大长方形的边长为a，小长方形的边长为b，则阴影部分的面积是a2-b2．若将图1中的阴影部分裁剪下来，重新拼成如图2的一个矩形，则它的面积是（a+b）（a-b）．
（2）有（1）可以得到乘法公式（a+b）（a-b）=a2-b2．
（3）若a=18，b=12，则请你求出阴影部分的面积．
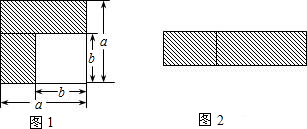
分析 （1）利用正方形的面积公式，图①阴影部分的面积为大正方形的面积-小正方形的面积，图②长方形的长为a+b，宽为a-b，利用长方形的面积公式可得结论；
（2）由（1）建立等量关系即可；
（3）将a=18，b=12，代入（a+b）（a-b）即可．
解答 解：（1）图①阴影部分的面积为：a2-b2，图②长方形的长为a+b，宽为a-b，所以面积为：（a+b）（a-b），
故答案为：a2-b2，（a+b）（a-b）；
（2）由（1）可得：（a+b）（a-b）=a2-b2，
故答案为：（a+b）（a-b）=a2-b2；
（3）将a=18，b=12，代入得：（18+12）（18-12）=180，
所以阴影部分的面积为：180．
点评 本题主要考查了平方差公式的推导过程，利用面积建立等量关系是解答此题的关键．
练习册系列答案
相关题目
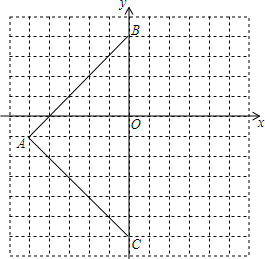如图，三角形ABC在平面直角坐标系中，三个顶点坐标分别为A（-5，-1）、B（0，4）、C（0，-6）．
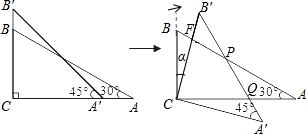如图所示，∠C=90°，Rt△ABC中，∠A=30°，Rt△A′B′C中，∠A=45°，点A′、B分别在线段AC、B′C上．将△A′B′C绕直角顶点C顺时针旋转一个锐角α时，边A′B′分别交AB、AC于P、Q，且△APQ为等腰三角形，则锐角α的度数15°．