题目内容
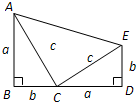 伽菲尔德( Garfield,1881年任美国第20届总统)利用“三个直角三角形的面积和等于一个直角梯形的面积”(如图所示)证明了勾股定理,请你应用此图证明勾股定理.
伽菲尔德( Garfield,1881年任美国第20届总统)利用“三个直角三角形的面积和等于一个直角梯形的面积”(如图所示)证明了勾股定理,请你应用此图证明勾股定理.
证明:如图,以a,b长为上下底边,以a+b长为高,作梯形ABDE,
即AB⊥BD,ED⊥BD,AB=a,ED=b,在其高BD上再取一点C,使BC=b,连结AC,EC,
在△ABC和△CDE中,
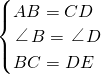 ,
,
∴△ABC≌△CDE(SAS),
∴AC=CE,∠BAC=∠DCE,
∴∠ACB+∠DCE=∠ACB+∠BAC=90°,
∴∠ACE=180°-(∠ACB+∠DCE)=180°-90°=90°,
∴△ACE为等腰直角三角形,设AC=c,
由梯形ABDE的面积公式得: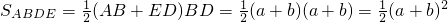 ,
,
梯形ABDE可分成如图所示的三个直角三角形,其面积又可以表示成:S△ABC+S△CDE+S△ACE=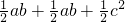 ,
,
∴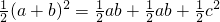 ,
,
∴a2+b2=c2.
即在直角△ABC中有a2+b2=c2(勾股定理).
分析:以a,b长为上下底边,以a+b长为高,作梯形ABDE,即AB⊥BD,ED⊥BD,AB=a,ED=b,在其高BD上再取一点C,使BC=b,连结AC,EC,求出△ACE是等腰直角三角形,根据梯形面积公式求出梯形面积,根据三角形面积公式求出梯形面积,即可得出等式,即可得出答案.
点评:本题考查了梯形面积,等腰直角三角形的性质和判定,三角形面积,全等三角形的性质和判定的应用,关键是能构造出能证出勾股定理的图形.
即AB⊥BD,ED⊥BD,AB=a,ED=b,在其高BD上再取一点C,使BC=b,连结AC,EC,
在△ABC和△CDE中,
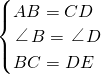 ,
,∴△ABC≌△CDE(SAS),
∴AC=CE,∠BAC=∠DCE,
∴∠ACB+∠DCE=∠ACB+∠BAC=90°,
∴∠ACE=180°-(∠ACB+∠DCE)=180°-90°=90°,
∴△ACE为等腰直角三角形,设AC=c,
由梯形ABDE的面积公式得:
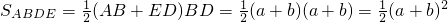 ,
,梯形ABDE可分成如图所示的三个直角三角形,其面积又可以表示成:S△ABC+S△CDE+S△ACE=
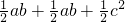 ,
,∴
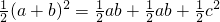 ,
,∴a2+b2=c2.
即在直角△ABC中有a2+b2=c2(勾股定理).
分析:以a,b长为上下底边,以a+b长为高,作梯形ABDE,即AB⊥BD,ED⊥BD,AB=a,ED=b,在其高BD上再取一点C,使BC=b,连结AC,EC,求出△ACE是等腰直角三角形,根据梯形面积公式求出梯形面积,根据三角形面积公式求出梯形面积,即可得出等式,即可得出答案.
点评:本题考查了梯形面积,等腰直角三角形的性质和判定,三角形面积,全等三角形的性质和判定的应用,关键是能构造出能证出勾股定理的图形.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 如图,AB是⊙O的直径,若∠C=26°,则∠ABD等于
如图,AB是⊙O的直径,若∠C=26°,则∠ABD等于

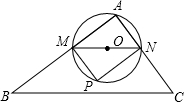 于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN,令AM=x.
于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN,令AM=x.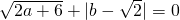 ,解关于x的不等式(a+2)x+b2>a-1.
,解关于x的不等式(a+2)x+b2>a-1.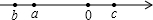
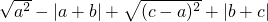 .
.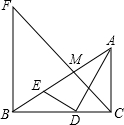 如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC交CM的延长线于点F
如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC交CM的延长线于点F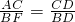 .
.