题目内容
解不等式与化简:
(1)已知a、b均为实数,且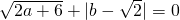 ,解关于x的不等式(a+2)x+b2>a-1.
,解关于x的不等式(a+2)x+b2>a-1.
(2)已知a,b,c在数轴上的位置如图所示,
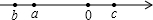
试化简: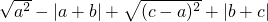 .
.
解:(1)∵ ≥0,|b-
≥0,|b- |≥0,
|≥0,
又∵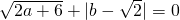 ,
,
∴ =0,|b-
=0,|b- |=0,
|=0,
解得 ,
,
将其代入不等式可得-x+2>-4,
解得x<6;
(2)由a,b,c在数轴上的位置,
可得b<a<0<c,
则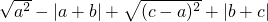
=-a-[-(a+b)]+(c-a)+[-(b+c)]=-a.
分析:(1)根据绝对值、算术平方根的性质(取值大于等于0)得 =0,|b-
=0,|b- |=0;故
|=0;故 .进而得出(a+2)x+b2>a-1的解集.
.进而得出(a+2)x+b2>a-1的解集.
(2)由a b c的大小关系化简可得.
点评:本题考查:(1)绝对值、算术平方根都是非负数;
(2)一元一次不等式的解法:一元一次不等式的解题思路有移项、化系数为1.
 ≥0,|b-
≥0,|b- |≥0,
|≥0,又∵
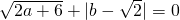 ,
,∴
 =0,|b-
=0,|b- |=0,
|=0,解得
 ,
,将其代入不等式可得-x+2>-4,
解得x<6;
(2)由a,b,c在数轴上的位置,
可得b<a<0<c,
则
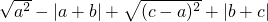
=-a-[-(a+b)]+(c-a)+[-(b+c)]=-a.
分析:(1)根据绝对值、算术平方根的性质(取值大于等于0)得
 =0,|b-
=0,|b- |=0;故
|=0;故 .进而得出(a+2)x+b2>a-1的解集.
.进而得出(a+2)x+b2>a-1的解集.(2)由a b c的大小关系化简可得.
点评:本题考查:(1)绝对值、算术平方根都是非负数;
(2)一元一次不等式的解法:一元一次不等式的解题思路有移项、化系数为1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 并把它的解集在数轴上表示出来
并把它的解集在数轴上表示出来
 并把它的解集在数轴上表示出来
并把它的解集在数轴上表示出来