Question

【题目】如图1，一次函数的图像与轴交于点，与轴交于点，过点作线段且，交轴于点．

（1）点的坐标轴__________，点的坐标轴__________；

（2）直接写出点的坐标轴__________，并求出直线的函数关系式；

（3）若点是图1中直线上的一点，连接，得到图2，当点在第二象限，且到轴，轴的距离相等时，直接写出的面积；

（4）若点是图1中坐标平面内不同于点、点的一点，当以点，，为顶点的三角形与全等时，直接写出点的坐标．

Answer 1

【答案】（1）；（2），；（3）3；（4）或或

【解析】

（1）将x=0和y=0分别代入一次函数解析式中，即可分别求出点A、B的坐标；

（2）过点C作CM⊥x轴于M，利用AAS证出△AOB≌△BMC，从而得出OB=CM=1，OA=MB=2，即可求出点C的坐标，然后设直线AC的解析式为y=kx＋b，将点A、C的坐标代入即可求出该解析式；

（3）过点P作PN⊥y轴于点N，根据题意可设点P的坐标为（-a， a），将点P代入直线AC的解析式中即可求出点P的坐标，从而求出PN的长，然后根据三角形的面积公式计算即可；

（4）先求出点D的坐标，然后根据点Q的位置和全等三角形的对应情况分类讨论，分别画出对应的图形，根据全等三角形的性质、等腰直角三角形的性质和平移规律分别求点Q的坐标即可．

解：（1）∵一次函数的图像与轴交于点，与轴交于点，

∴当x=0时，解得y=2；当y=0时，解得x=1

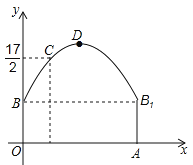
∴点A的坐标为（0,2），点B的坐标为（1,0）

故答案为：（0,2）；（1,0）；

（2）过点C作CM⊥x轴于M

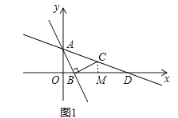
∴∠AOB=∠BMC=∠ABC=90°

∴∠OAB＋∠ABO=90°，∠MBC＋∠ABO=180°－∠ABC=90°

∴∠OAB=∠MBC

在△AOB和△BMC中

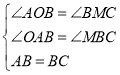
∴△AOB≌△BMC

∴OB=CM=1，OA=MB=2

∴OM=OB＋MB=3

∴点C的坐标为（3,1）

故答案为：（3,1）；

设直线AC的解析式为y=kx＋b

将A、C两点的坐标代入，得

解得：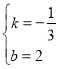

∴直线AC的解析式为

（3）过点P作PN⊥y轴于点N

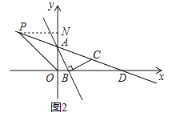
∵点在第二象限，且到轴，轴的距离相等

可设点P的坐标为（-a， a）

将点P的坐标代入直线AC的解析式中，得

解得：

∴点P的坐标为（-3，3）

∴PN=3

∴S△AOP=OA·PN=×2×3=3

（4）将y=0代入直线AC的解析式中，解得x=6

∴点D的坐标为（6,0）

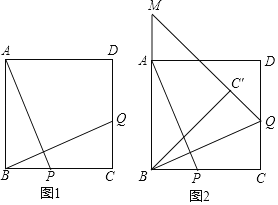
①当点Q在直线AC的上方，且△QDC≌△BCD时，如下图所示

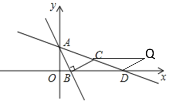
∴∠BDC=∠QCD，CQ=BD=6－1=5

∴CQ∥x轴

∴点Q可看成由点C向右平移5个单位长度

∴此时点Q的坐标为（8,1）；

②当点Q在直线AC的上方，且△QCD≌△BCD时，如下图所示

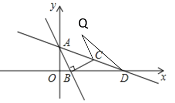
∴QC = BC，∠QCD=∠BCD

∴∠QCA=∠BCA

∵∠ABC=90°，BA=BC

∴△ABC为等腰直角三角形，QC=BA

∴∠BAC=∠BCA=∠QCA=45°

∴QC∥AB

∴QC可看成AB平移得出

∵点B（1,0）到点C（3,1）的平移方式为：先向右平移2个单位，再向上平移1个单位

∴点Q是由点A（0,2）先向右平移2个单位，再向上平移1个单位

∴此时点Q的坐标为（2,3）；

③当点Q在直线AC的下方，且△QDC≌△BCD时，如下图所示

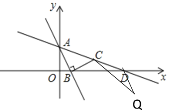
∴QD=BC，∠QDC=∠BCD

∵∠ABC=90°，BA=BC

∴△ABC为等腰直角三角形，QD=BA

∴∠BAC=∠BCA =45°，

∴∠BCD=180°－∠BCA=135°

∴∠QDC=135°

∴∠QDC＋∠BAC=180°

∴QD∥BA

∴QD可看成BA平移得出

∵点A（0,2）到点D（6,0）的平移方式为：先向右平移6个单位，再向下平移2个单位

∴点Q是由点B（1,0）先向右平移6个单位，再向下平移2个单位

∴此时点Q的坐标为（7,-2）；

④当点Q在直线AC的下方，且△QCD≌△BCD时，此时点Q与点B重合，不符合题意，舍去．

综上所述：点Q的坐标为或或．