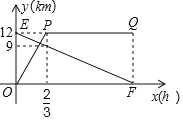
题目内容
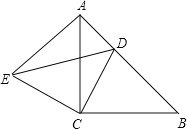
【题目】如图，
中，
，
，
，
，
，
，
是直线
上一点，把
沿
所在的直线翻折后，点
落在直线
上的点
处，
的长是__________
【答案】
或
【解析】
根据折叠后点C的对应点H与AC的位置关系分类讨论，分别画出对应的图形，利用勾股定理求出各边的长，再根据折叠的性质与勾股定理列出对应的方程即可求出结论．
解：①当折叠后点C的对应点H在AC的下方时，如下图所示
∵
中，
，
，
，
根据勾股定理可得BC=
∵
，
，
∴
，
∵
根据勾股定理可得DE=
由折叠的性质可得：DH=CD=，CP=PH
∴EH=DH－DE=
设CP=PH=x，则EP=CE－CP=－x
在Rt△PEH中，EP2＋EH2=PH2
即（－x）2＋（）2=x2
解得：x=
即此时CP=；
②当折叠后点C的对应点H在AC的上方时，如下图所示
根据折叠的性质可得DH=CD=，CP=PH
∴EH=DH＋DE=
设CP=PH=y，则EP= CP－CE =y－
在Rt△PEH中，EP2＋EH2=PH2
即（y－）2＋（）2=y2
解得：y=
即此时CP=．
综上所述：CP=或．
故答案为：或．
练习册系列答案
相关题目
