题目内容
【题目】如图在△ABC中，∠B=50°，∠C=30°，分别以点A和点C为圆心，大于AC的长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，连接AD，
（1）若△ABD的周长是19，AB=7，求BC的长；
（2）求∠BAD的度数．
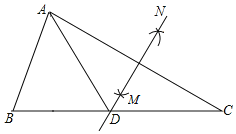
【答案】（1）BC=12；（2）∠BAD=70°
【解析】
（1）根据作图明确MN是线段AC的垂直平分线,得AD=DC，结合△ABD的周长和AB的长度即可得出BC的长度；
（2）根据作图明确MN是线段AC的垂直平分线,得∠C=∠DAC=30°,利用内角和求出∠BAC=100°,进而求出∠BAD=70°.
（1）由图可知MN是AC的垂直平分线
∴AD=DC．
∵△ABD的周长=AB+AD+BD=19，AB=7
∴7+DC+BD=7+BC=19．
∴BC=12．
（2）∵∠B=50°，∠C=30°
∴∠BAC=100°．
∵MN是AC的垂直平分线
∴AD=DC．
∴∠DAC=∠C=30°．
∴∠BAD=∠BAC-∠DAC=100°-30°=70°．
【题目】某校要从甲、乙两名同学中挑选一人参加创新能力大赛，在最近的五次选拔测试中， 他俩的成绩分别如下表，请根据表中数据解答下列问题：
第 1 次 | 第 2 次 | 第 3 次 | 第 4 次 | 第 5 次 | 平均分 | 众数 | 中位数 | 方差 | |
甲 | 60 分 | 75 分 | 100 分 | 90 分 | 75 分 | 80 分 | 75 分 | 75 分 | 190 |
乙 | 70 分 | 90 分 | 100 分 | 80 分 | 80 分 | 80 分 | 80 分 |
（1）把表格补充完整：
（2）在这五次测试中，成绩比较稳定的同学是多少；若将 80 分以上（含 80 分） 的成绩视为优秀，则甲、乙两名同学在这五次测试中的优秀率分别是多少；
（3）历届比赛表明，成绩达到80分以上（含 80分）就很可能获奖，成绩达到 90分以上（含90分）就很可能获得一等奖，那么你认为选谁参加比赛比较合适？说明你的理由．
