题目内容
9．2a2-4ab+5b2-8a-4b+2004的最小值是1984．分析 观察2a2-4ab+5b2-8a-4b+2004式子要求其最小值，只要将所有含有a、b的式子转化为多个非负数与常数项的和的形式．一般常数项即为所求最小值．
解答 解：2a2-4ab+5b2-8a-4b+2004，
=（a2-4ab+4b2）+（a2-8a+16）+（b2-2b+4）+1984，
=（a-2b）2+（a-4）2+（b-2）2+1984≥1984，
则-4ab+5b2-8a-4b+2004的最小值是1984．
故答案是：1984．
点评 本题考查了完全平方公式、非负数的性质．解决本题的关键是将所有含有a、b的式子都转化为多个非负数与常数项的和形式．
练习册系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
相关题目
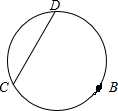如图，已知CD是圆中的弦，B为圆上一点，且$\widehat{BC}$=$\widehat{BD}$．
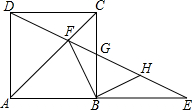如图，E为正方形ABCD的边AB延长线上一点，DE交AC于点F，交BC于点G，H为GE的中点，求证：FB⊥BH．
19．小明、小联、小豪人一起玩“剪刀、石头、布”的游戏．每一局三人同时出“剪刀、石头、布”中的一种手势．则小明只赢一人的概率为（ ）
| A． | $\frac{2}{9}$ | B． | $\frac{4}{9}$ | C． | $\frac{2}{27}$ | D． | $\frac{4}{27}$ |