题目内容
16.(1)$\frac{{sin{{45}°}+cos{{30}°}}}{{3-2cos{{60}°}}}-sin{60°}(1-sin{30°})$(2)$\frac{{sin{{30}°}}}{{sin{{60}°}-cos{{45}°}}}-\sqrt{{{(1-tan{{60}°})}^2}}-tan{45°}$.
分析 (1)将特殊角的三角函数值代入求解;
(2)将特殊角的三角函数值代入求解.
解答 解:(1)原式=$\frac{\frac{\sqrt{2}}{2}+\frac{\sqrt{3}}{2}}{3-1}$-$\frac{\sqrt{3}}{2}$(1-$\frac{1}{2}$)
=$\frac{\sqrt{2}}{4}$+$\frac{\sqrt{3}}{4}$-$\frac{\sqrt{3}}{4}$
=$\frac{\sqrt{2}}{4}$;
(2)原式=$\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}-\frac{\sqrt{2}}{2}}$-($\sqrt{3}$-1)-1
=$\sqrt{3}$+$\sqrt{2}$-$\sqrt{3}$
=$\sqrt{2}$.
点评 本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.

练习册系列答案
相关题目
4.每天你是如何醒来的?某校有4000名学生,从不同班级不同层次抽取了400名学生进行调查,下表是这400名学生早晨起床方式的统计表:
回答下列问题:
(1)该问题中总体是某校4000名学生早晨起床的情况;
(2)样本是400名学生早晨起床的情况;样本的容量是400;
(3)个体是每一名学生早晨起床的情况;
(4)估计全校学生中自己醒来的人数为640人.
| 起床方式 | 人数 |
| 别人叫醒 | 172 |
| 闹钟 | 88 |
| 自己醒来 | 64 |
| 其它 | 76 |
(1)该问题中总体是某校4000名学生早晨起床的情况;
(2)样本是400名学生早晨起床的情况;样本的容量是400;
(3)个体是每一名学生早晨起床的情况;
(4)估计全校学生中自己醒来的人数为640人.
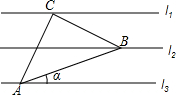 已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个项点分别在这三条平行直线上,则sinα的值是$\frac{\sqrt{10}}{10}$.
已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个项点分别在这三条平行直线上,则sinα的值是$\frac{\sqrt{10}}{10}$.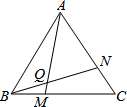 如图,已知△ABC中,AB=BC=AC,∠ABC=∠BCA=∠CAB=60°,M、N分别在△ABC的BC、AC边上,且BM=CN,AM、BN交于点Q.求证:∠BQM=60°.
如图,已知△ABC中,AB=BC=AC,∠ABC=∠BCA=∠CAB=60°,M、N分别在△ABC的BC、AC边上,且BM=CN,AM、BN交于点Q.求证:∠BQM=60°. 在△ABC中,已知AB=13,BC=10,BC边上的中线AD=12. 试说明:AB=AC.
在△ABC中,已知AB=13,BC=10,BC边上的中线AD=12. 试说明:AB=AC.