题目内容
 如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=128°,∠C=36°,∠DAE
如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=128°,∠C=36°,∠DAE考点:三角形内角和定理
专题:
分析:根据角平分线的定义可得∠CAE=
∠BAC,再根据直角三角形两锐角互余求出∠CAD,然后根据∠DAE=∠CAE-∠CAD代入数据计算即可得解.
| 1 |
| 2 |
解答:解:∵AE是△ABC的角平分线,
∴∠CAE=
∠BAC=
×128°=64°,
∵AD⊥BC,
∴∠CAD=90°-∠C=90°-36°=54°,
∴∠DAE=∠CAE-∠CAD=64°-54°=10°.
故答案为:10.
∴∠CAE=
| 1 |
| 2 |
| 1 |
| 2 |
∵AD⊥BC,
∴∠CAD=90°-∠C=90°-36°=54°,
∴∠DAE=∠CAE-∠CAD=64°-54°=10°.
故答案为:10.
点评:本题考查了三角形的内角和定理,角平分线的定义,熟记定理和概念并准确识图,判断出∠DAE=∠CAE-∠CAD是解题的关键.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案
相关题目
若a<3,则
=( )
| (a-3)2 |
| A、a+3 | B、a-3 |
| C、-a-3 | D、-a+3 |
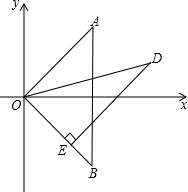 如图,等腰直角△OAB的直角顶点O是坐标原点,顶点在一、三象限的角平分线上,顶点B在第四象限,Rt△ODE的直角顶点E在直线OB上,且OD=4,∠ODE=30°,将Rt△ODE绕点O顺时针旋转15°,得到Rt△OD1E1,线段D1E1交直线OB于点F.若某反比例函数的图象经过点F,则这个反比例函数的解析式为
如图,等腰直角△OAB的直角顶点O是坐标原点,顶点在一、三象限的角平分线上,顶点B在第四象限,Rt△ODE的直角顶点E在直线OB上,且OD=4,∠ODE=30°,将Rt△ODE绕点O顺时针旋转15°,得到Rt△OD1E1,线段D1E1交直线OB于点F.若某反比例函数的图象经过点F,则这个反比例函数的解析式为 如图,小明从点A出发,沿直线前进20m后向左转30°,再沿直线前进20m,又向左转30°…照这样走下去,小明第一次回到出发点A,一共走了
如图,小明从点A出发,沿直线前进20m后向左转30°,再沿直线前进20m,又向左转30°…照这样走下去,小明第一次回到出发点A,一共走了