题目内容
3.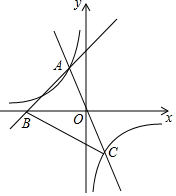 如图,在平面直角坐标系中,直线y=x+3与x轴交于点B,与直线OA交于点A,反比例函数y=$\frac{k}{x}$经过点A,与直线OA的另一个交点为C,连接BC,已知tan∠AOB=2.
如图,在平面直角坐标系中,直线y=x+3与x轴交于点B,与直线OA交于点A,反比例函数y=$\frac{k}{x}$经过点A,与直线OA的另一个交点为C,连接BC,已知tan∠AOB=2.(1)求直线OA和反比例函数的解析式;
(2)求△ABC的面积.
分析 (1)利用待定系数法求两函数的解析式;
(2)根据面积和求△ABC的面积.
解答  解:(1)当x=0时,y=3,
解:(1)当x=0时,y=3,
∴OE=3,
当y=0时,x+3=0,
x=-3,
∴B(-3,0),
∴OB=3,
∴OB=OE=3,
∵∠BOE=90°,
∴△BOE是等腰直角三角形,
过A作AD⊥x轴于D,则△ADB也是等腰直角三角形,
∵tan∠AOB=$\frac{AD}{OD}$=2,
∴AD=2OD,
设OD=x,则AD=2x,BD=3-x,
∵AD=BD,
∴2x=3-x,
x=1,
∴A(-1,2),
设直线OA的解析式为:y=ax(a≠0),
把A(-1,2)代入得:2=-a,
a=-2,
∴直线OA的解析式为:y=-2x,
∵反比例函数y=$\frac{k}{x}$经过点A,
∴k=-1×2=-2,
∴反比例函数的解析式为:y=-$\frac{2}{x}$;
(2)由题意得:$\left\{\begin{array}{l}{y=-2x}\\{y=-\frac{2}{x}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=-2}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-1}\\{{y}_{2}=2}\end{array}\right.$,
∴C(1,-2),
∴S△ABC=S△AOB+S△BOC=$\frac{1}{2}$×3×2+$\frac{1}{2}$×3×2=6.
点评 本题考查了利用待定系数法求函数的解析式、三角函数、等腰直角三角形的性质和判定、三角形面积、函数的交点问题,利用三角函数及等腰直角三角形的性质确定AD=BD,列方程是关键.

练习册系列答案
相关题目
11.学校举行演讲比赛,有6名选手参加选拔赛,所得分数各不相同,按成绩取前3名进入决赛.小明也参加了选拔,他要判断自己能否进入决赛,只需知道这次6名选手分数的( )
| A. | 方差 | B. | 平均数 | C. | 众数 | D. | 中位数 |
18.在数轴上表示不等式x>-3的解集,正确的是( )
| A. |  | B. |  | C. |  | D. |  |
 转动如图所示的转盘,当转盘停止转动时,求转得下列各数的概率.
转动如图所示的转盘,当转盘停止转动时,求转得下列各数的概率.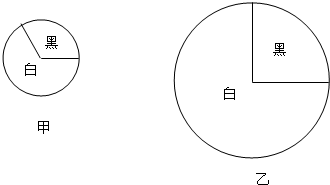 如图,有甲、乙两个圆,它们的半径之比为3:8,每个圆又都被分割成黑、白两个扇形,其中甲圆被分成的黑、白两个扇形的面积之比为1:2,乙圆被分成的黑、白两个扇形的面积之比为1:3,那么图中两个黑色扇形的面积之和与两个白色扇形的面积之和的比是19:54.(直接写出答案)
如图,有甲、乙两个圆,它们的半径之比为3:8,每个圆又都被分割成黑、白两个扇形,其中甲圆被分成的黑、白两个扇形的面积之比为1:2,乙圆被分成的黑、白两个扇形的面积之比为1:3,那么图中两个黑色扇形的面积之和与两个白色扇形的面积之和的比是19:54.(直接写出答案)