题目内容
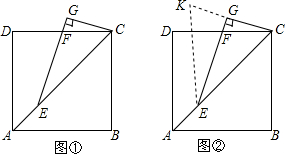
20. 如图,P是矩形ABCD的边BC上一点.EP⊥AP,EP分别交边AC,CD于点F,E
如图,P是矩形ABCD的边BC上一点.EP⊥AP,EP分别交边AC,CD于点F,E(1)求证:△ABP∽△PCE;
(2)若P是BC中点,BC=2AB,AB=2,求PF的长.
分析 (1)根据矩形的性质得到∠B=∠BCD=90°,根据余角的性质得到∠BAP=∠EPC,即可得到结论;
(2)根据矩形的性质得到AB=CD,AD=BC,∠ABC=∠DCB=90°,根据已知条件得到AB=PB=PC=CD,由余角的性质得到∠APB=∠DPC=45°,推出点D,E重合,根据勾股定理得到AP=2$\sqrt{2}$,AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=2$\sqrt{5}$,通过△ADF∽△PCF,根据相似三角形的性质得到$\frac{AF}{CF}=\frac{AD}{CP}$=2,求得AF=$\frac{4\sqrt{5}}{3}$,然后又勾股定理即可得到结论.
解答 解:(1)∵四边形ABCD是矩形,
∴∠B=∠BCD=90°,
∵EP⊥AP,
∴∠BAP+∠APB=∠APB+∠EPC=90°,
∴∠BAP=∠EPC,
∴△ABP∽△CPE;
(2)如图,
∵四边形ABCD是矩形,
∴AB=CD,AD=BC,∠ABC=∠DCB=90°,
∵P是BC中点,BC=2AB,
∴AB=PB=PC=CD,
∵EP⊥AP,
∴∠APD=90°,∴∠APB=∠DPC=45°,
∴点D,E重合,
∵AB=2,
∴BC=AD=4,
∴AP=2$\sqrt{2}$,AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=2$\sqrt{5}$,
∵AD∥BC,
∴△ADF∽△PCF,
∴$\frac{AF}{CF}=\frac{AD}{CP}$=2,
∴AF=$\frac{4\sqrt{5}}{3}$,
∴PF=$\sqrt{A{F}^{2}-A{P}^{2}}$=$\frac{2\sqrt{2}}{3}$.
点评 此题考查了矩形的性质,以及相似三角形的判定与性质,勾股定理,等腰直角三角形的性质,熟练掌握矩形的性质是解本题的关键.

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,AD=AC,∠DAB=∠CAB,则判断△DAB≌△CAB的最快理由是( )
如图,AD=AC,∠DAB=∠CAB,则判断△DAB≌△CAB的最快理由是( )| A. | SSS | B. | SAS | C. | HL | D. | ASA |

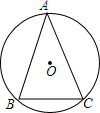 如图所示,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠B=70°,则$\widehat{BC}$的度数=80°.
如图所示,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠B=70°,则$\widehat{BC}$的度数=80°.