Question

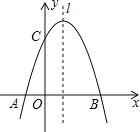
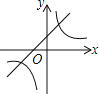
【题目】如图，在平面直角坐标系中，一次函数y=x+b的图象经过点A（-2,0），与反比例函数 的图象交于B（a，4）．

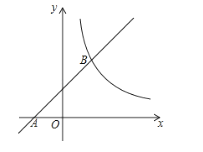
(1)求一次函数和反比例函数的表达式；

(2)根据图像，写出不等式的解集；

(3)设M是直线上一点，过M作MN∥x轴，交反比例函数的图象于点N，若点M的横坐标为m，且MN=4，求m的值．

Answer 1

【答案】（1）y=x+2 ,；（2）；（3）m的值为0.

【解析】

（1）根据一次函数y=x+b的图象经过点A(2,0)，可以求得b的值，从而可以解答本题；

（2）根据图像，即可直接写出解集.
（3）根据题意分别得出M,N的坐标，再根据MN∥x轴，得出两个点的纵坐标相等，即可解出m的值.

（1）一次函数y=x+b的图象经过点A（-2,0），

0=-2+b，得b=2，

一次函数的解析式为y=x+2.

一次函数的解析式为y=x+2与反比例函数的图象交于B（a，4），

4=a+2，得a=2，

4=，得，

即反比例函数解析式为：.

（2）a=2

B（2，4）

根据图像，不等式的解集为

（3）M是直线y=x+2上一点，且点M的横坐标为m

点M的坐标为（m,m+2）

又MN∥x轴，交反比例函数的图象于点N，且MN=4

点N的坐标为（m+4，）

且M,N纵坐标相等

即

解得：m=0或-6（不符合题意舍去）

综上m的值为0.