题目内容
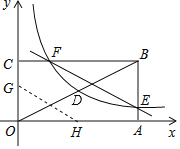
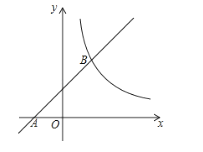
【题目】如图,已知抛物线![]() 与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0)
与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0)
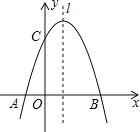
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
(3)点M是抛物线在第一象限内图像上的任意一点,求当BCM的面积最大时点M的坐标.
【答案】(1)m=2,顶点坐标为(1,4);(2)点P(1,2);(3)![]()
【解析】
(1)将点B的坐标为(3,0)代入解析式中,即可求得m的值,然后利用顶点坐标公式求得抛物线的顶点坐标;
(2)根据A、B关于抛物线的对称轴对称,先连接BC交抛物线对称轴于点P,则此时PA+PC的值最小,然后利用待定系数法求得直线BC的解析式,从而求出P点坐标;
(3)过M点作MD⊥x轴交BC与点D,利用M、D所在的图像设出坐标,再利用“铅垂高水平宽”求出面积与坐标的关系,最后利用顶点坐标求最值即可.
解:(1)将点B的坐标为(3,0)代入解析式中得:
![]()
解得:m=2
故抛物线的解析式为:![]()
顶点坐标的横坐标为:![]() ,代入解析式中得y=4
,代入解析式中得y=4
∴抛物线的顶点坐标为:(1,4);
(2)∵根据A、B关于抛物线的对称轴对称
∴连接BC交抛物线对称轴于点P,则此时PA+PC的值最小,
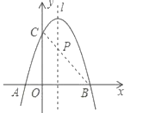
将x=0代入到![]() 中,得:
中,得:![]()
∴点C的坐标为(0,3)
设直线BC的解析式为:y=kx+b,
将B、C的坐标分别代入得:
![]()
解得:![]()
所以直线BC的解析式为:y=-x+3
将x=1代入到y=-x+3得:y=2
∴P点坐标为(1,2)
(3)过M点作MD⊥x轴交BC与点D,设M的坐标为![]() ,D的坐标为
,D的坐标为![]() ,C到MD的距离为h1,B到MD的距离为h2,由图可知h1+ h2=OB=3
,C到MD的距离为h1,B到MD的距离为h2,由图可知h1+ h2=OB=3
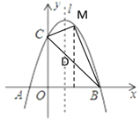
∴MD=![]()
∴SBCM=SDCM+SBDM=![]()
∵![]()
∴当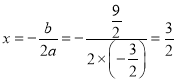 时,SBCM有最大值,
时,SBCM有最大值,
将![]() 代入
代入![]() 中,得:
中,得:![]() ,
,
故当BCM的面积最大时点M的坐标为:![]()