Question

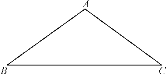
【题目】如图，在△ABC中，AB＝AC＝5，BC＝8，将△ABC绕着点B旋转得到△A′BC′，点A的对应点A′，点C的对应点C′.如果点A′在BC边上，那么点C和点C′之间的距离为____.

Answer 1

【答案】.

【解析】

作AD⊥BC于D，C′E⊥BC于E，如图1，先利用等腰三角形的性质得到 再利用勾股定理计算出AD=4，接着利用旋转的性质得A′B=A′C′=AB=5，△A′BC′≌△ABC，则利用面积法可求出C′E，然后在Rt△A′C′E中利用勾股定理计算A′E，于是可在Rt△C′CE中利用勾股定理计算出CC′．

解：作AD⊥BC于D，C′E⊥BC于E，如图1，

∵AB=AC，

在Rt△ABD中，

∵△ABC绕着点B旋转的△A′BC′，

∴A′B=A′C′=AB=5，△A′BC′≌△ABC，

∴A′C=3，S△A′BC′=12，

而

∴解得

在Rt△A′C′E中，

在Rt△C′CE中，

故答案为.