题目内容
 如图,在等边△ABC中,AB=2,D是BC上一动点,过点D作DE⊥AC于点E,求AD+DE的最小值.
如图,在等边△ABC中,AB=2,D是BC上一动点,过点D作DE⊥AC于点E,求AD+DE的最小值.考点:轴对称-最短路线问题
专题:
分析:利用等边三角形的性质结合函数性质画出函数图象,进而分析求出最值即可.
解答:
 解:设BD为x,作AF⊥BC于F,
解:设BD为x,作AF⊥BC于F,
∵AC=AB=BC=2,
∴FC=1,
∴AF=
,BF=1,
所以DF=1-x,
所以AD2=(1-x)2+3,AD=
CD=2-x,DE=
(2-x),
所以AD+DE=
+
(2-x),(0≤x≤2),
如图所示:当x=2时,AD+DE最小为:2.

 解:设BD为x,作AF⊥BC于F,
解:设BD为x,作AF⊥BC于F,∵AC=AB=BC=2,
∴FC=1,
∴AF=
| 3 |
所以DF=1-x,
所以AD2=(1-x)2+3,AD=
| x2-2x+4 |
CD=2-x,DE=
| ||
| 2 |
所以AD+DE=
| x2-2x+4 |
| ||
| 2 |
如图所示:当x=2时,AD+DE最小为:2.
点评:此题主要考查了轴对称最短路线问题,利用函数图象分析得出是解题关键.

练习册系列答案
相关题目
 如图,△ABC中,AB=AC,∠C=70°,则∠B的度数为( )
如图,△ABC中,AB=AC,∠C=70°,则∠B的度数为( )| A、60° | B、70° |
| C、75° | D、80° |
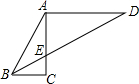 如图,在Rt△ABC中,∠C=90°,AD∥BC,∠CBE=
如图,在Rt△ABC中,∠C=90°,AD∥BC,∠CBE=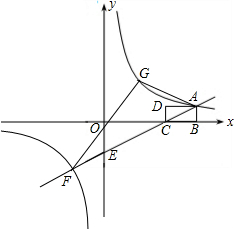 如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,一次函数y=kx-2的图象经过点A、C,并与y轴交于点E.反比例函数y=
如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,一次函数y=kx-2的图象经过点A、C,并与y轴交于点E.反比例函数y= 已知E为平行四边形ABCD外一点,AE⊥CE,BE⊥DE,求证:平行四边形ABCD是矩形.
已知E为平行四边形ABCD外一点,AE⊥CE,BE⊥DE,求证:平行四边形ABCD是矩形.