��Ŀ����
�Ķ����н����̣�Ȼ��ش����⣮��֪����ʽx3+4x2+mx+5��һ����ʽ��x+1������m��ֵ��
��������
����һ����ʽΪ��x2+ax+b����
��x3+4x2+mx+5=��x+1����x2+ax+b��=x2+��a+1��x2+��a+b��x+b��
��a+1=4��a+b=m��b=5����a=3��b=5����m=8��
��������Ľⷨ��������⣺��x3+3x2��3x+k��һ����ʽ��x+1����k��ֵ��
-5. �������������������һ������ʽ���ɼ�������ʽ����ʽ�˻�����ʽʱ�������һ����ʽΪ��ʱ������������ʽ��ֵΪ��.�����м���x+1=0���x��ֵ���Ӷ���x��ֵ�������ʽ���k��ֵ. ����������߶���ʽx3+4x2+mx+5��һ����ʽ��x+1���� ����x+1=0��x=��1������x=��1ʱ��ԭ����ʽΪ�㣬 �ࣨ��1��3+3������1��2��3������1��+k=0�� ��k=��...
��ϰ��ϵ�д�
�����Ŀ


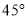 �ǵ�ֱ�����ǰ壬����һ����Ƕ���
�ǵ�ֱ�����ǰ壬����һ����Ƕ���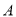 �ڰ뾶Ϊ
�ڰ뾶Ϊ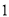 �ġ�
�ġ�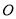 �ϣ���
�ϣ���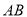 ��
�� 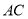 �ֱ����
�ֱ����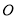 ���ڵ�
���ڵ�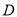 ��
�� 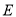 ����
���� �ij�Ϊ__________��
�ij�Ϊ__________��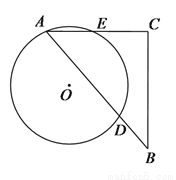
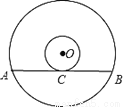
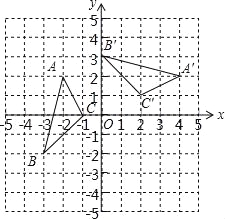
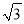 B.
B. 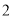 C.
C. 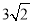 D.
D. 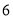
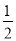 S��ABC������������ʼ����ȷ�� ��������
S��ABC������������ʼ����ȷ�� ��������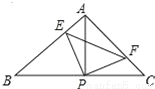
 ��
��