题目内容
求证:两条平行线的一对同位角的角平分线互相平行.
考点:平行线的判定与性质
专题:证明题
分析:根据题意画出图形,写出已知与求证,证明过程为:由AM与BN平行,利用两直线平行同位角相等得到一对角相等,再由AE与BF为角平分线,利用角平分线定义及等量代换得到一对同位角相等,利用同位角相等两直线平行可得出AE与BF平行,得证.
解答:解:已知,AM∥BN,AE为∠CAM的平分线,BF为∠ABN的平分线,如图所示,

求证:AE∥BF.
证明:∵AM∥BN(已知),
∴∠CAM=∠ABN(两直线平行,同位角相等),
∵AE为∠CAM的平分线,BF为∠ABN的平分线(已知),
∴∠CAE=
∠CAM,∠ABF=
∠ABN(角平分线定义),
∴∠CAE=∠ABF(等量代换),
∴AE∥BF(同位角相等,两直线平行).

求证:AE∥BF.
证明:∵AM∥BN(已知),
∴∠CAM=∠ABN(两直线平行,同位角相等),
∵AE为∠CAM的平分线,BF为∠ABN的平分线(已知),
∴∠CAE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠CAE=∠ABF(等量代换),
∴AE∥BF(同位角相等,两直线平行).
点评:本题考查了平行线的性质和判定的应用,对于文字叙述型题,首先根据题意画出图形,根据图形写出已知,求证,最后写出证明过程即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
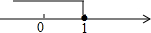 下列说法错误的是( )
下列说法错误的是( )| A、不等式x-3<-2的解集为x<1 |
| B、不等式x+2≤-2的最大负整数解为-1 |
| C、若不等式-3x+7<-2x成立,则不等式2x>9成立 |
| D、不等式-x≥-1的解集表示在数轴上如图所示 |
 如图,已知⊙O中,直径BC平分∠ABD,求证:
如图,已知⊙O中,直径BC平分∠ABD,求证:
