题目内容
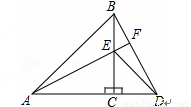
如图,在△ABC中,∠A=30°,∠B=45°,AC=2 ,则AB的长为 .
,则AB的长为 .

3+
【解析】
试题分析:过C作CD⊥AB于D,求出∠BCD=∠B,推出BD=CD,根据含30度角的直角三角形求出CD,根据勾股定理求出AD,相加即可求出答案.
过C作CD⊥AB于D,
∴∠ADC=∠BDC=90°,
∵∠B=45°,
∴∠BCD=∠B=45°,
∴CD=BD,
∵∠A=30°,AC=2 ,
,
∴CD= ,
,
∴BD=CD= ,
,
由勾股定理得:AD= =3,
=3,
∴AB=AD+BD=3+ ,
,
答:AB的长是3+ .
.

考点:1. 解直角三角形;2.等腰三角形的性质;3.含30度角的直角三角形;4.勾股定理.

练习册系列答案
相关题目



 B.
B.  C.
C.  D.
D. 
 分别是△
分别是△ 的边
的边 和
和 上的点,
上的点, ,
, ,要使
,要使 ∥
∥ ,
, 应等于 ;
应等于 ;
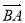 =
=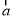 ,
,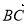 =
=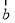 ,试用
,试用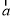 、
、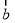 分别表示向量
分别表示向量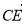 和
和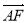 .
. 