题目内容
4.已知Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,根据下列条件判断第三边是否是有理数,(1)a=2,b=3,c不是有理数;
(2)a=5,b=12,c是有理数.
分析 (1)已知两直角边求斜边,利用勾股定理求得c,再根据有理数的定义即可求解;
(2)已知两直角边求斜边,利用勾股定理求得c,再根据有理数的定义即可求解.
解答 解:∵Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,
∴(1)a=2,b=3,c=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,c不是有理数;
(2)a=5,b=12,c=$\sqrt{{5}^{2}+1{2}^{2}}$=13,c是有理数.
故答案为:不是,是.
点评 本题考查了利用勾股定理解直角三角形的运算能力.勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.

练习册系列答案
相关题目
14.方程x2-2x-5=0经配方后,可化为( )
| A. | (x-1)2=6 | B. | (x+1)2=6 | C. | (x-1)2=4 | D. | (x+1)2=4 |
14.如果m:n=2:3,则下列各式不成立的是( )
| A. | $\frac{m+1}{n+1}$=$\frac{3}{4}$ | B. | $\frac{n-m}{n}$=$\frac{1}{3}$ | C. | $\frac{3m}{2n}$=1 | D. | $\frac{m+n}{n}$=$\frac{5}{3}$ |
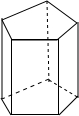 如图所示的是一个五棱柱.它的底面边长都是4cm.侧棱长都是6cm.
如图所示的是一个五棱柱.它的底面边长都是4cm.侧棱长都是6cm.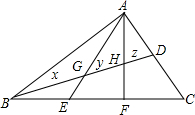 如图,D是AC的中点,E,F是BC的三等分点,设BG=x,GH=y,HD=z,则x:y:z=5:3:2.
如图,D是AC的中点,E,F是BC的三等分点,设BG=x,GH=y,HD=z,则x:y:z=5:3:2. 如图,OP平分∠AOB,PC⊥OA于点C,PD⊥OB于点D,CD与OP相交于点Q.求证:CQ=DQ.
如图,OP平分∠AOB,PC⊥OA于点C,PD⊥OB于点D,CD与OP相交于点Q.求证:CQ=DQ.