题目内容
17.已知正三角形的边长为2$\sqrt{3}$,求它的边心距、半径、周长和面积.分析 先求出边长为6的正三角形的周长,再由三角函数求出边心距,得出外接圆的半径,再求出其面积即可.
解答 解:如图所示: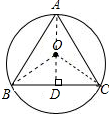
连接OA、OB、OC,过O作OD⊥BC于D,
∵△ABC是边长为2$\sqrt{3}$的等边三角形,
∴AB=AC=BC=2$\sqrt{3}$,∠ABC=60°,
∴△ABC的周长=3AB=6$\sqrt{3}$,∠OBD=30°,
∵OD⊥BC,
∴∠ODB=90°,BD=CD=$\frac{1}{2}$BC=$\sqrt{3}$,
∴OD=BD•tan30°=$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=1,
∴OB=2OD=2,
∴AD=OA+OD=3,
∴△ABC的面积=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×2$\sqrt{3}$×3=3$\sqrt{3}$,
即正三角形的周长为6$\sqrt{3}$,边心距为1,半径为2,面积为3$\sqrt{3}$.
点评 本题考查的是正三角形的性质、边心距、半径、周长和面积的计算;熟练掌握正三角形的性质,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.用配方法解方程x2-8x+7=0,配方后正确的是( )
| A. | (x-4)2=7 | B. | (x-4)2=11 | C. | (x-4)2=9 | D. | (x+4)2=7 |
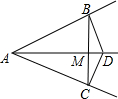 点D是∠BAC的平分线上一点,过点D作DB⊥AB于点B,DC⊥AC于点C,连接BC交AD于点M.求证:
点D是∠BAC的平分线上一点,过点D作DB⊥AB于点B,DC⊥AC于点C,连接BC交AD于点M.求证: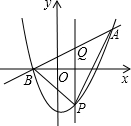 如图,二次函数y=$\frac{1}{2}$x2+bx+c的图象与x轴交于B、C两点(点B在点C的左侧),一次函数y=kx+1的图象经过点B和二次函数图象行另一点A.其中点A的坐标为(4,3).
如图,二次函数y=$\frac{1}{2}$x2+bx+c的图象与x轴交于B、C两点(点B在点C的左侧),一次函数y=kx+1的图象经过点B和二次函数图象行另一点A.其中点A的坐标为(4,3).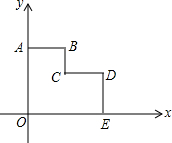 如图,在平面直角坐标系xOy中,多边形OABCDE的顶点分别为O(0,0)、A(0,8)、B(4,8)、C(4,4)、D(8,4)、E(8,0),若直线l经过点M(3,$\frac{7}{2}$),分别与边OA、DE相交且将多边形OABCDE面积平分.
如图,在平面直角坐标系xOy中,多边形OABCDE的顶点分别为O(0,0)、A(0,8)、B(4,8)、C(4,4)、D(8,4)、E(8,0),若直线l经过点M(3,$\frac{7}{2}$),分别与边OA、DE相交且将多边形OABCDE面积平分.