题目内容
7.观察下列因式分解的过程:①x2+5x+4=(x2+4x)+(x+4)=x(x+4)+(x+4)=(x+1)(x+4);
②x2-2x-3=x2-3x+x-3=x(x-3)+(x-3)=(x+1)(x-3);
③x2-2x-8=x2-4x+2x-8=x(x-4)+2(x-4)=(x+2)(x-4);
根据上述因式分解的方法,尝试将下列各式进行因式分解.
x2-4x-5=(x-5)(x+1);
x2-6x+5=(x-1)(x-5);
x2-xy-6y2=(x-3y)(x+2y).
分析 根据阅读材料中的方法,将原式各项分解即可.
解答 解:x2-4x-5=(x-5)(x+1);
x2-6x+5=(x-1)(x-5);
x2-xy-6y2=(x-3y)(x+2y).
故答案为:(x-5)(x+1);(x-1)(x-5);(x-3y)(x+2y).
点评 此题考查了因式分解-十字相乘法,熟练掌握十字相乘的方法是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.计算:
(1)(x2-2x)•x2;
(2)-2x2y3(x-1);
(3)3x(2x+y)-2x(x-y);
(4)(-$\frac{1}{2}$ab)($\frac{2}{3}$ab2-2ab+1)
(1)(x2-2x)•x2;
(2)-2x2y3(x-1);
(3)3x(2x+y)-2x(x-y);
(4)(-$\frac{1}{2}$ab)($\frac{2}{3}$ab2-2ab+1)
12.扎西把含糖为6%和12%的两种饮料倒在一起,配成了含糖8%的混合饮料240g.那么含糖6%和12%两种饮料分别用了( )
| A. | 80g,160g | B. | 160g,80g | C. | 120g,120g | D. | 200g,40g |
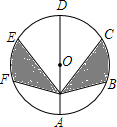 如图所示,AD是⊙O的直径,A,B,C,D,E,F顺次六等分⊙O,已知⊙O的半径为1,P为直径AD上任意一点,求图中阴影部分的面积.
如图所示,AD是⊙O的直径,A,B,C,D,E,F顺次六等分⊙O,已知⊙O的半径为1,P为直径AD上任意一点,求图中阴影部分的面积.